おっと危ない：信頼区間と予測区間を混同しちゃダメ

今回は仕事で解析をしていて「おっと危ない」と思ったことについて書いてみます。結論からいうと「信頼区間と予測区間を混同しないように注意しましょう！」という話です*1。

課題：BODの値からTOCの値を推定したい

最近ややあってBOD（生物化学的酸素要求量）の値からTOC（全有機炭素量）の値を推定してみようと思いました*2。
試しに東京都の15地点から得られている水質データを用いてRで両者の散布図を描いてみると以下のようになりました（データはこちら：BOD-TOC.txt ）。相関はあるものの、バラツキもかなりあります。

BOD2TOC.data <- read.table("BOD-TOC.txt",sep=",")
TOC <- BOD2TOC.data$TOC
BOD <- BOD2TOC.data$BOD
plot(BOD,TOC,type="p",xlim=c(0,6),ylim=c(0,6),lty=2,ylab="",xlab="")

一般にTOCとBODのあいだは基本的には相関関係が期待されるものの、その関係は含まれる有機物の性質の違いなどにも強く依存するらしいので（解説の例）、まあ実際こんなかんじが実態として妥当なところなのでしょう*3。

試行：線形回帰で信頼区間を計算する

とりあえず、Rのlm()で線形回帰してみました*4：

> res.lm <- lm(TOC ~ BOD)> summary(res.lm)
Call:
lm(formula = TOC ~ BOD)

Residuals:
     Min       1Q   Median       3Q      Max
. -1.55509 -0.63353 -0.09311  0.51785  3.24216

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  1.44825    0.12087   11.98   <2e-16 ***
BOD          0.60959    0.05915   10.31   <2e-16 ***



-

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8136 on 186 degrees of freedom
Multiple R-squared: 0.3635,     Adjusted R-squared: 0.3601
F-statistic: 106.2 on 1 and 186 DF,  p-value: < 2.2e-16

切片と傾きはとても有意ですが、R2乗値は0.36（=相関係数は0.6）と低いです。

もともとの目的はBODの値からTOCの値を推測することなので、例としてBOD=3mg/LのときのTOCの推定値とその95%信頼区間を計算してみましょう。predict()を使います：

> predict(res.lm, new=data.frame(BOD=c(3)), interval="confidence")
fit       lwr       upr
3.27701  3.092730  3.461290

BOD=3mg/LのときのTOCの値の95%信頼区間は3.09〜3.46mg/Lと推定することができそうです。
あれ？予想外に推定の精度が高くないですか？ラッキー！

では、回帰直線とその95%信頼区間を散布図に重ねて描いてみましょう。

> new <- data.frame(BOD = seq(0.1,8,0.1))
> pred.lm <- predict(res.lm, new, interval="confidence")
> 
> x.plot <- seq(0.1,8,0.1)
> plot(x.plot,pred.lm[,1],type="l",xlim=c(0,6),ylim=c(0,6),ylab="")
> par(new=T)
> plot(x.plot,pred.lm[,2],type="l",xlim=c(0,6),ylim=c(0,6),lty=2,col="red",ylab="")
> par(new=T)
> plot(x.plot,pred.lm[,3],type="l",xlim=c(0,6),ylim=c(0,6),lty=2,col="red",ylab="")
> par(new=T)
> plot(BOD,TOC,type="p",xlim=c(0,6),ylim=c(0,6),lty=2,ylab="TOC",xlab="BOD")
> par(new=F)

ん？ぜんぜん信頼区間（赤線）が散布図のバラツキと合ってないですよね。。。何かがおかしい？

疑問：それって「何の」信頼区間？

上記の例で信頼区間が散布図のバラツキと合っていないのは実は当然です。上で描かれている信頼区間は「回帰直線の信頼区間」であるからです。

「回帰直線の信頼区間」というのは、「もし上記のような測定・解析を全く同じやり方で100回繰り返したら、100回のうち95回は回帰直線はこの範囲を通ると考えられますよ」という区間という意味です。

また、ある特定のBODの値において予測される値の話でいうと、「上記のような測定・解析を全く同じやり方で100回繰り返したら、BOD=3mg/LのときTOCの「平均値」は100回に95回は「3.09〜3.46mg/L」の値の範囲に収まりますよ」ということを示していることになります*5。

なので、上の図での回帰直線（あるいはある特定のBODに対するTOCの「平均値」）の信頼区間が、標本全体のバラツキに比べて小さいというのは当然のことになります。標準誤差（母数のuncertaintyに関わる）が標準偏差（標本のvariabilityに関わる）より小さいのと同じようなことです*6（＊両者の違いについてはこちら； "uncertainty"と"variability"というリスク学用語についてはこちら＊）。

解決：予測区間を計算する

BOCの値からTOCの値を推測する際に、最終的にリスクの最尤値だけを問題とするならば「TOCの平均値」だけを扱っても良いかもしれませんが、一般にリスク評価では推測の際の不確実性も考慮することが非常に大切です。

特に、上述の線形回帰ではR2乗値が0.36でしたので、得られた線形モデルではデータ内に存在するバラツキ（不確実性）のうち36%しか考慮できていません。残りの64%のバラツキ（不確実性）は残差のまま取りこぼされています。この64%を無視したまま得られた回帰直線（およびその信頼区間）を用いてリスク推定を行ってしまうと、リスク推定の精度が実際よりもかなり高く水増しされてしまうことになります。

そこで、回帰直線のまわりの残差によるバラツキも考慮した「（平均値ではなく）個々のTOCの予測値」の予測範囲を考えましょう。そのような値は「新たな測定を行ったときに予測される値」として解釈でき*7、その値の範囲は「予測区間」と呼ばれます。Rでは、predict.lm()の引数として「interval="prediction"」と指定すれば求めることができます：

pred.lm <- predict(res.lm, new, interval="prediction")

x.plot <- seq(0.1,8,0.1)
plot(x.plot,pred.lm[,1],type="l",xlim=c(0,6),ylim=c(0,6),ylab="")
par(new=T)
plot(x.plot,pred.lm[,2],type="l",xlim=c(0,6),ylim=c(0,6),lty=2,col="red",ylab="")
par(new=T)
plot(x.plot,pred.lm[,3],type="l",xlim=c(0,6),ylim=c(0,6),lty=2,col="red",ylab="")
par(new=T)
plot(BOD,TOC,type="p",xlim=c(0,6),ylim=c(0,6),lty=2,ylab="",xlab="")
par(new=F)

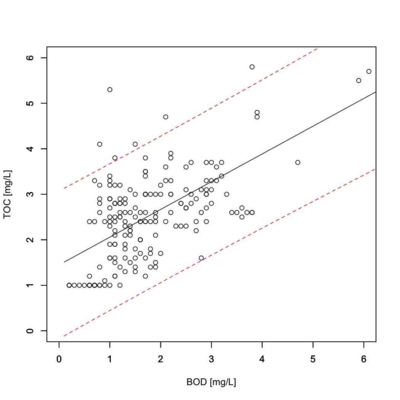
今度は予測区間の範囲と散布図のバラツキの範囲が概ね一致しました。BOD=3mg/LのときのTOCの95%予測区間は「1.66〜4.89mg/L」になります。直感的にも妥当なかんじですね。

まあ理想論からいえば「R2乗値が0.36のモデルをリスク評価に使っちゃだめ」というのも正解かもしれませんが、上記の解析から「TOCの値はBODの値からマイナス1.4〜プラス1.9mg/Lくらいの範囲に概ね収まると予測されます」というくらいのザックリしたことは言えるかと思います。用途によっては、これくらいザックリしたことが言えるだけでも上出来といえるでしょう*8。

議論：「モデル」と「値そのもの」のどちらに興味があるのか確認しよう

では、「信頼区間」と「予測区間」はどのように使い分けたらいいのでしょうか？

結論からいうと、興味の対象が「モデル」あるいは「モデルの母数」にあるなら「信頼区間」を使うことになると思います。一方、興味の対象が「個々の値そのもの」である場合には「予測区間」を使うのが妥当になるでしょう。

上記の場合は「個々のBOCの値から個々のTOCの値を推測すること」が目的なので、興味の対象は「個々の値（TOC）」となり、「予測区間」を用いるのが妥当となります。

教訓：信頼区間からの「安全側」の値をインプットに用いてリスク計算するとかなりマズイ

リスク評価の実務では、実測値が得られないデータについて統計的に推測し、その推測値をシミュレーションモデルなどの入力値として用いてリスクの計算を行うということが日常的に行われます。

そのリスク計算において「リスク推定の不確実性」を適切に考慮するためには、その推測値の計算にともなうモロモロの不確実性もモンテカルロシミュレーションなどの手法で入力値の「不確実性」として入れてやらなければいけません。もし今回のような場合に、「回帰直線の信頼区間」を「個々の値の予測区間」と混同して使用してしまうと、最終的に得られるリスク評価結果の精度が本来よりもかなり水増しされてしまうので、かなりマズイことになります。

また、リスク評価では「安全側」の判断として、推定される値の「区間」の下限から「安全側」の推定値を採用するということがよく行われます*9。このような場合、「回帰直線の信頼区間」の下限から選んだ「安全側」の値は、「予測区間」の下限から選んだ本来の「安全側」の値よりもかなり「危険側」に寄ってしまうので、これもかなりマズイことになってしまいます。

さらに、「回帰直線の信頼区間」を「予測区間」と混同していると、その路の専門家が見れば一目で分かる直感的にもおかしい予測精度になってしまいがちなので、こんな予測をペロッと採用していたら利害関係者からの信用をいっぺんに失いかねません。リスク評価は信用されてナンボなので、こういうポカは極力避けなければいけません。

ついついウッカリするとこの辺りはミスしがちなところなので気をつけたいものです。あと、基本中の基本ですが、ミスを避けるためには計算結果をいちいち散布図などと重ねてみるのがやっぱり大事*10、というのも今回の教訓かもしれません。