なぜ無作為化なのか：『因果推論の根本問題』とその解法

こんにちは。林岳彦です。はてなジョシュ（バーネット）です。今回から「はてなブログ」へ引っ越しました。今後とも引きつづきよろしくお願いします。

さて。

前回までの記事では、実験データではない調査観察データを用いた因果効果の推定における注意すべきバイアスの類型について書いてきました。

ここでなぜわざわざ「実験データではない」という但し書きをつけているのかというと、適切なデザインに基づき行われた実験（もしくは介入を伴う調査）からのデータは、処理・条件の違いによる結果の差を素直に「因果効果」とみなして解釈できるので、余り細かいことを考えなくても大丈夫だからです*1。

はい。

では、そもそも、なぜそのような実験では「結果の差を素直に因果効果とみなせる」のでしょうか？

今回は、その背景となるロジックについて書いていきたいと思います。

（すみません今回もものすごく長いです。。。）

まずは「因果効果」を定義してみる：「職業訓練が将来の年収に与える効果」を例に

はい。そもそも「因果効果」って何でしょうか。

論理学者でも無ければ抽象的なままに考えていくのはなかなか難しいので、今回は「職業訓練が将来の年収に与える影響」の例を通して考えていきたいと思います。

あなたの親友Kが失業しており、行政による職業訓練プログラムを受講するかどうか迷っているとします。このとき、判断の材料としては色々ありうるかとは思われますが、「その職業訓練が親友Kの将来の年収を増やすと期待できるのか」という点は重要といえるでしょう。

このとき、「職業訓練→親友Kの将来の年収」の”因果効果”を言葉で定義すると以下のように表現できるかと思います：

職業訓練を受講した場合の親友Kの5年後の年収　ー　職業訓練を受講しない場合の親友Kの5年後の年収

職業訓練を受講した場合に収入が伸びればこの"因果効果"はプラスになりますし、職業訓練を受講した場合に収入が減ればこの"因果効果”はマイナスになります。（ここでは、「将来の年収」については便宜的に”5年後の"年収を指標とすることにします）

ちなみに、上の例をより一般的な形で表現すると、対象Xに対する「処理A→結果Z」の"因果効果"は：

対象Xに処理Aを行った場合の結果Z　ー　対象Xに処理Aを行わない場合の結果Z

と表すことができるでしょう。

ここまでは、感覚的にも理解しやすいかと思います。

しかしながら。

上記の「因果効果」は、本質的に”不可知"なのです。

「因果効果」は不可知である：『因果推論の根本問題』

なぜ不可知なのか。

それは：

職業訓練を受講した場合の親友Kの5年後の年収　ー　職業訓練を受講しない場合の親友Kの5年後の年収

の、両者の「場合」を共に観察することはできないからです。

つまり、「親友Kが職業訓練を受講した場合」には「職業訓練を受講しない場合の親友Kの5年後の年収」を知ることはできませんし、同様に「親友Kが職業訓練を受講しない場合」には「職業訓練を受講した場合の親友Kの5年後の年収」は知ることはできないのです。

身も蓋もない話ですが、まあ、そうですよね。

なので、上記の「因果効果」はそもそも知ることができないシロモノなのです。

「因果推論」において横たわるこの本質的な問題は『因果推論の根本問題（The fundamental problem of causal inference）』と呼ばれており、まあ基本的には途方に暮れるしかない問題です。

だがしかし。いつかはゆかし。むかしむかし統計学の世界にはロナルド・フィッシャーという途方も無い天才がおりまして、この『根本問題』に対する"銀の弾丸"を遺してくれました。それが、「無作為化」というアイデアです。

以下では、そのアイデアについて（すこし回り道をしながら）説明していきます。

さてどうするか：「集団への因果効果」を考えてみる

まずは、『因果推論の根本問題』への対処として、「集団への因果効果」を考えてみることにします。

統計学の基本的な考え方は「多くの事例を見れば法則が見えてくるかも（帰納法）」なので、"親友K”ひとりではなく、「職業訓練を受講した人／しない人」の多くの事例を集めることにより、「職業訓練→将来の年収」の「因果効果」に迫ることを試みてみましょう。

まず、調査への協力者をn人集めたとします。ここで、各個人i（n=1,…,n）への"因果効果"は以下のように定義できるでしょう：

職業訓練を受講した場合の個人iの5年後の年収　ー　職業訓練を受講しない場合の個人iの5年後の年収

はい。これは、平たく言うと「（個人iにおける）職業訓練の受講の有無による5年後の年収の差」になります。残念ながら、この"因果効果"は上記の『根本問題』で見たとおり、知ることのできないシロモノです。

では、各個人ではなく、「n人の5年後の”平均”年収」に着目し「集団への”平均"因果効果」を以下のように定義してみます：

職業訓練を受講した場合のn人の5年後の平均年収　ー　職業訓練を受講しない場合のn人の5年後の平均年収

はい。こちらは、n人の"集団"で見た時の「職業訓練の受講の有無による5年後の平均年収の差」になっています。

さて。

実は、ここで、「集団への"平均"因果効果」を考えてみても、『根本問題』はちっとも解決されていません。（すみません。。）

なぜなら、「n人が職業訓練を受講した場合」には「職業訓練を受講しない場合のn人の5年後の平均年収」は知ることができませんし、「n人が職業訓練を受講しない場合」には、「職業訓練を受講した場合のn人の5年後の平均年収」は知ることができないからです。

さて。もう少し考えを進めてみましょう。

全員について知る必要はない：n人を2つの「グループ」に分けてみる

次善の策を練ってみましょう。

「職業訓練を受講した場合のn人の5年後の平均年収」と「職業訓練を受講しない場合のn人の5年後の平均年収」を同時に知ることができないのなら、n人を「職業訓練を受講した人のグループ」と「職業訓練を受講しない人のグループ」に分けて考えれば良いのかもしれません。

ここでn人の内訳として、「職業訓練を受講した」グループがm人、「職業訓練を受講しない」グループがk人いたとしましょう（n=m+kとする）。

このとき、「職業訓練→将来の年収」の因果効果を：

職業訓練を受講したm人の5年後の平均年収　ー　職業訓練を受講しないk人の5年後の平均年収

という形で捉えることはできるでしょうか？

うむ。

これは、できそうな気もします。少なくとも、この場合には第1項と第2項の両方の量を（原理的には）知ることができるという点では現実的と言えます。

しかしながら、これはこれで、問題が生じます。

なぜなら、「職業訓練を受講したm人」と「職業訓練を受講しないk人」の両者のグループには、かなり性質の違う人々が含まれている可能性があるからです。

例えば、「行政による職業訓練プログラムを受講した人のグループ」の中には、そもそもの流れとして現在失業中の人々が相対的に多く含まれているかもしれませんし、「受講しない人のグループ」の中には、現状のところは安定した職を得ている、もしくは専門的スキルが既にある人々が相対的に多く含まれているかもしれません。

このように両者のグループの性質が異なりうる場合には：

職業訓練を受講したm人の5年後の平均年収　ー　職業訓練を受講しないk人の5年後の平均年収

という量を計算したところで、それが「職業訓練→将来の年収」の因果効果に起因するものなのか、「グループ間のそもそもの性質の違い」に起因するものなのか、うまく判別がつきません。

いたしかゆしです。

ではここで一旦、ちょっと理屈っぽい話となりますが、この状況を俯瞰してみることにします。

問題を俯瞰する：「反事実」の世界へようこそ

上記の状況を、Rubinの反事実モデルの枠組みを用いて整理してみます。

今まで見てきた職業訓練の例では、処理（条件）として「職業訓練を受講した／受講しない」の２つの場合、帰結として「職業訓練を受講した場合の5年後の年収／受講しない場合の5年後の年収」の２つの場合がありました。

これら「条件」と「帰結」の組み合わせを表にまとめると、論理的には、以下の4種類の「平均年収データ」がありうることになります：

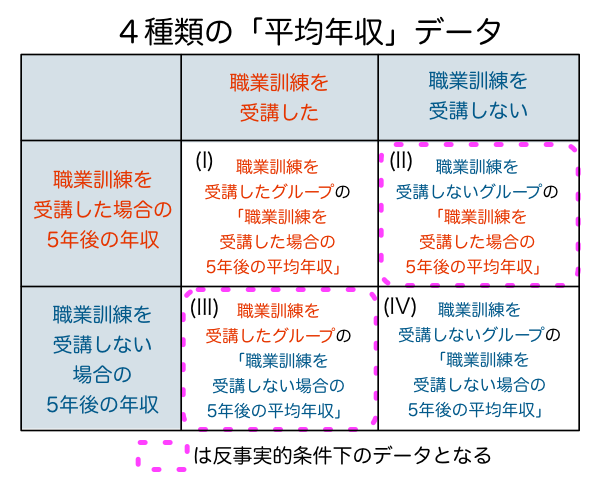
上の図の4種類の「平均年収データ」について書き下すと：

(I) 職業訓練を受講したグループの「職業訓練を受講した場合の5年後の平均年収」
(II) 職業訓練を受講しないグループの「職業訓練を受講した場合の5年後の平均年収」
(III) 職業訓練を受講したグループの「職業訓練を受講しない場合の5年後の平均年収」
(IV) 職業訓練を受講しないグループの「職業訓練を受講しない場合の5年後の平均年収」

となります。

一見とてもややこしいですが、(I)と(IV)の「平均年収データ」については、特に問題はないかと思います。文として素直に意味が通ってますし、実際にデータを得ることも（少なくとも原理的には）可能です。

一方、(II)(III)の「平均年収データ」は、原理的に「そもそも観測することができないデータ」となっています。「職業訓練を受講したグループ」についての「職業訓練を受講しない場合の5年後の年収」はそもそも観測することができませんし、同様に「職業訓練を受講しないグループ」についての「職業訓練を受講した場合の5年後の年収」も観測することができません。

(II)(III)のようなデータは「事実に反した条件（counterfactual condition）」の下でしか得られないデータとなります。つまり、ここでは：

「職業訓練を受講しないグループ」が”もし職業訓練を受けていたとしたとき”の、5年後の平均年収」

という形で、「（事実としては受講していないけれども）もし職業訓練を受けていたとしたとき」という、反事実的な状況が想定されていることになります。

はい。

ここで重要なポイントを2つまとめます：

(1) 「因果効果」の推論においては、必然的に「反事実的状況下のデータ」の値を知る必要がある
(2) われわれが現実的に得られるのは、「事実として起きた状況」のもとでのデータのみである

この(1)については、「職業訓練→年収」の因果効果というのが「(I) と (III)の差」、つまり

　(I) 職業訓練を受講したグループの「職業訓練を受講した場合の5年後の平均年収」
　ー　 (III) 職業訓練を受講したグループの「職業訓練を受講しない場合の5年後の平均年収」

で定義されることに対応します*2。この後者の項は、反事実的状況下でのみ得られるデータとなっています。

(2)については、いわずもがなですが、われわれが得ることができるのは(I)と(IV)の状況下のデータのみである、ということです。

これらのポイントを図中にまとめると：

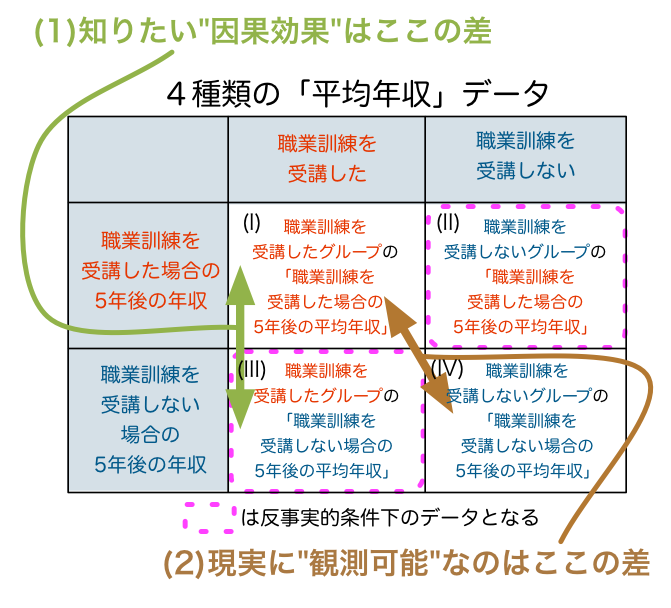
という状況であると言えます。

このような状況を前にして、"事実的世界"に存在する我々が目指しうるゴールは：

反事実的世界においてしか観測できない(III)のデータを、現実に観測可能な(I)や(IV)のデータを用いて”観測”する

ことになるわけです。

どうやるのかって？

ここで、"無作為化”の出番です。

その銀の弾丸を放て：無作為化により『根本問題』を解く

さて。

反事実的世界においてしか観測できない(III)のデータを、現実に観測可能な(I)や(IV)のデータを用いて”観測”する

ためにはどうすれば良いでしょうか。

ここで、「（III)と(IV)の値が一致すると期待できるような条件」を考えてみます。

この(III)と(IV)で異なる部分は、「受講したグループ」と「受講しないグループ」の部分です。そこで、最初に職業訓練を受けてもらう前の段階で、「両者のグループの間に差がでないようなやり方」でn人のグループ分けを行うことにしましょう。

ここで、「両者のグループに差がでないようなやり方」として最も汎用的な方法が、「無作為化」です。

例えば、集まってもらったn人にコインを投げてもらい、オモテが出た人は「受講するグループ」になり職業訓練を受講してもらい、ウラが出た人は「受講しないグループ」になり職業訓練を受講しないでいてもらいます。（このように各個体に対して無作為に条件や処理のグループを割り付けることを「無作為割付」と言います）

このとき、「受講するグループ」と「受講しないグループ」の間には本質的な差は無いと考えられるので、理屈として、5年後の年収データとしての

(IV) 職業訓練を受講しないグループの「職業訓練を受講しない場合の5年後の平均年収」

の期待値は

(III) 職業訓練を受講したグループの「職業訓練を受講しない場合の5年後の平均年収」

の期待値と一致すると考えられます。なぜなら、両グループは単にコイントスで分けただけなので、（もし値が測定可能であった場合に）両者の値（の期待値）に差が出ると考えるべき理由が何もないからです。（例えば、両者のグループの「身長の平均値」の期待値が異なるとは考えられないですよね。それと理屈的には同じです。また、数式を用いた補遺を記事末尾に載せましたので適宜ご参照ください。）

もちろん実際には(III)のデータは反事実的なので得ることはできません。しかし、無作為化（コイントス）によりグループを分けた場合には、(III)と(IV)の「平均年収」の期待値は理屈的に一致すると考えられるので、ここで「(III)のデータの身代わりとして(IV)のデータを使う」という"迂回路"が使えるようになるわけです。

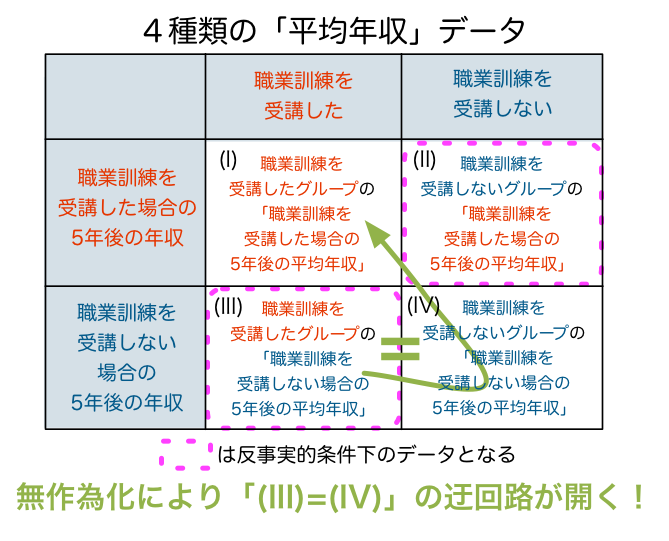
この"迂回路"を使うことにより、

　(I) 職業訓練を受講したグループの「職業訓練を受講した場合の5年後の平均年収」
　ー　 (III) 職業訓練を受講したグループの「職業訓練を受講しない場合の5年後の平均年収」

という不可知な項を含む"因果効果”を

　(I) 職業訓練を受講したグループの「職業訓練を受講した場合の5年後の平均年収」
　ー　 (IV) 職業訓練を受講しないグループの「職業訓練を受講しない場合の5年後の平均年収」

と読み替えることが可能になるわけです。これらの(I)と(IV)の量は観測可能なデータなので、この読み替えを行うことにより、「職業訓練→将来の年収」の"因果効果”を推定することができることになります。

はい。

これで、『因果推論の根本問題』を統計学的に解くことができました。（これが、いわゆる『統計学的因果推論』というものの一例となります）

（ただし、ここで推定できたのはあくまで集団への「"平均的"因果効果」であることに注意してください。そもそもの話である、職業訓練が「親友K」に与える因果効果は、やはり不可知なままなのです。たとえ職業訓練の"平均"効果がプラスであったとしても、親友Kにはそれがマイナスに働く可能性は常に残ります。個体に対する因果効果は、本質的にやはり不可知なのです。）

まとめ

ではまとめます。

今回は以下のようなことを見てきました：

そもそも：因果推論を行うためには、「反事実的状況下におけるデータ」を観測する必要がある
ゆえに：因果推論は不可能である（『因果推論の根本問題』）
しかし：無作為化により、「反事実的データ」の身代わりに観測可能なデータを使うことができる（『根本問題』の統計学的解決）
なかにし：「無作為化ハンパないって　反事実的なデータめっちゃトラップするもん」
かんとく：「おれ握手してもらったぞ」

はい。

一見地味に感じるかもしれませんが、「ランダムネス」の意図的な利用により「法則」を浮かび上がらせるというこの「無作為化というアイデア」はなかなかに凄いものであるようにも思います。かのリチャード・ドーキンスが「ダーウィン以降で最も偉大な生物学者」としてフィッシャーの名を挙げていましたが、この「無作為化というアイデア」はその「ダーウィン以降で最も偉大な生物学者」が遺したものの中でも、「最も偉大な発明」の一つと言えるかもしれません。

そんなわけで、「統計的因果推論」の分野で有名な研究者といえば、RubinやPearlの名が挙がるのかもしれませんが、「統計的因果推論のキング」を一人選ぶとしたらやはりフィッシャーになるのではないかと思います。

はい。

というわけで、『統計学の道を歩むかぎり、お天道様とフィッシャーはどこへいってもついてまわる』という格言を再認識したところで、今回の記事も終わろうかと思います*3。

＃次回からは、そろそろ「確率概念」についてガッツリ書いていこうかなあ、と思ってます。

補遺(1)：無作為化のキモについて

上記の説明では、「コイントス」を用いて無作為化を行っていますが、別にそこは必ずしも「コイントス」でなくとも構いません。大事なことは、割付（＝各人をどのグループに分けるのか）を、「受講した場合／しない場合の5年後の平均年収」と本来的に全く関係ない（＝独立な）要素にもとづき決めるということです。

数式で書くと、上記の表の

(III) 職業訓練を受講したグループの「職業訓練を受講しない場合の5年後の平均年収」
(IV) 職業訓練を受講しないグループの「職業訓練を受講しない場合の3年後の平均年収」

の期待値は、それぞれ

(III) E(職業訓練を受講しない場合の5年後の平均年収｜職業訓練を受講したグループに割付された）
(IV) E(職業訓練を受講しない場合の5年後の平均年収｜職業訓練を受講しないグループに割付された）

と書けます。ここでE(A|B)という表記は、「Bという条件」の下での「Aの期待値」を表しています。

ここで、「B」の条件がAと全く関係ない（＝独立な）要素によって決められている場合には、E(A|B)=E(A)となるため：

(III) E(職業訓練を受講しない場合の5年後の平均年収｜職業訓練を受講したグループに割付された）＝ E(職業訓練を受講しない場合の5年後の平均年収）
(IV) E(職業訓練を受講しない場合の5年後の平均年収｜職業訓練を受講しないグループに割付された）＝E(職業訓練を受講しない場合の5年後の平均年収）

となり、「(III)の期待値＝(IV)の期待値」となるわけです。

ここのキモは「Bの条件がAと全く関係ない（＝独立な）要素によって決められている」ことなので、コイントスやサイコロを使わずとも、例えば「各人の携帯電話番号の末尾が偶数か奇数か」にもとづき職業訓練受講の有無（B）の条件を割りつけても、E(A|B)=E(A)を満たすと考えられるので問題ありません。

逆に、職業訓練を受講していない場合の5年後の平均年収（A）と潜在的に関係のある要素に基づき割付を行うと、E(A|B)=E(A)が満たされないので因果推論がうまくいきません*4。例えば、「現在求職中かどうか」にもとづき職業訓練受講の有無（B）の条件を割りつけると、BとAは独立でない可能性が高く、E(A|B)=E(A)は満たされないでしょう。

また、細かい話になりますが、条件Bを無作為に割付けたとしても、「条件を割付けたこと自体」がAに影響を及ぼす場合は、E(A|B)=E(A)が満たされないのでやはりダメです。例えば、「訓練を受講するグループに割り付けられた」こと自体がモチベーションを変化させ、（実際の訓練受講とは関係ない部分で）年収に影響を与えてくる場合には、BとAは独立とならず、E(A|B)=E(A)は満たされません。このような場合はいわゆるSUTVA違反のケースに相当します*5。

補遺(2)：無作為化ができないときにはその悲しみをどうすりゃいいの？誰がぼくを救ってくれるの？

正直どうにもならないことも多いですが、とりあえず「傾向スコア」とか「バックドア基準」とかを参照してみてください。

統計的因果推論（傾向スコア）の勉強会資料をアプしてみた - Take a Risk：林岳彦の研究メモ
 発表資料アプ『相関と因果について考える：統計的因果推論、その(不)可能性の中心』 - Take a Risk：林岳彦の研究メモ

===【20180806追記ここから】======================
久しぶりに読み返したところ、上の記述に対しては「サッパリすぎるだろ」と思ったので追記しておきます。無作為化が成立しているか怪しいときは「まずバックドアパスを閉じれるように工夫してみて、それでも閉じれているかどうか分からないときには想定されるバックドアパスの「太さ」について定量的に考察してみましょう（感度分析など）」となるかなあと思います。簡単にあきらめないで！

＊とりあえず以下の良記事を参照すると吉：
www.krsk-phs.com
www.krsk-phs.com
===【20180806追記ここまで】======================

詳しくは、以下の参考文献を読むのをオススメいたします。