内生性・交絡 revisited：説明変数と残差と誤差の相関をのんびり眺めるの巻

こんにちは。林岳彦です。ggplot2を使いこなすシャレオツな若い人を見ると自分の老いを感じる今日このごろです。

さて。

今回は、「説明変数と誤差項に相関がある」とはどういうことか、について見ていきたいと思います。

経済学系の統計解析の本を読んでいると「内生性」という概念がよく出てきます（経済学系でない分野においては、「交絡」と呼ばれるものに実務上はおおむね対応する概念と言えます）。

この「内生性」の説明としては、例えば：

計量経済モデルにおいて、説明変数と誤差項との間に相関があるときに、内生性（endogeneity）があるという。このとき、説明変数は内生的（endogenous）であることになる。説明変数が内生的であれば、推定されたパラメータは一致推定量ではなくなり、推定値は統計学的に信頼されるものとはなりえない。

のように説明されます（内生性 - Wikipediaより引用*1。強調は引用者による）。

お分かりになりましたでしょうか。

うーん。このように「説明変数と誤差項との間に相関があるとき」とペロっと言われても、それはいったい内実としてどういうことなのでしょうか？ ここはちょっと直感的には掴みづらいところがあります。説明変数と誤差項との相関。やれやれ。村上春樹の小説の主人公ならばそう呟くところかと思われます*2。

少なくとも、私も長らくのあいだ「頭では概念として理解はできるけども、なんか腑に落ちた気がしないんだよなあ！」みたいなかんじでモヤモヤを抱えてきました。（一般的な傾向として、「交絡」の概念の方により親しんでいる人々にとっては「内生性」の概念はにわかに掴みづらいところがあると思います）

なので今回、「説明変数と誤差項に相関がある」という現象について、具体的な数値例と数式と散布図などを行き来しながら一度のんびりと眺めてみようと思いました。

以下はその観察記録です。あと、私はRの作図用パッケージであるggplot2を余り使ったことがなかったのでその練習も兼ねております。なんか、ggplot2を使う若者が、眩しかったので。

いつもながらめちゃくちゃ長い記事となっておりますが誠に申し訳ありません（一二塁間を鋭く転がるゴロに対して菊池涼介が飛びつくイメージで土下座）。もしご興味のある方はあくまでごゆるりとご参照いただければと思います。

注：以下の内容では特に何か新奇なことが書いてあるわけではありませんが、例えばもしあなたが「内生性があるとき、説明変数と残差の間には相関はありますか？」と聞かれて即答できなかったり、即答できたとしてもその話と「誤差」と「残差」の関係についてモヤモヤが残るようであれば、以下の内容を読むことで何らかの気付きがあるかもしれません。

まずそもそも：回帰分析の「誤差項」って何だろう？

まずちょっと誤差項について「そもそも」的な話をしておきたいと思います。「説明変数と誤差項の間に相関がある」という話が直感的に飲み込みにくい理由のひとつは、「誤差」という語の一般的なイメージにあるように思います。

分野と文脈にもよるかもしれませんが、一般に「誤差」という語は「偶然により生じるバラツキ」という意味内容で用いられることが多いかと思います*3。

この「誤差＝偶然によるバラツキ」のイメージだと、「説明変数」と「誤差項」が相関する、と言われてもちょっと直感的には分かりにくいかもしれません。「偶然」なのに「相関」する、というのはちょっとモヤモヤしますよね。偶然と相関は別ではない、むしろその一部として存在するのだ。村上春（以下略）

実際には、回帰分析における「誤差項」というのは、「偶然によるバラツキ」というよりも「回帰モデル内に含まれていない要因に起因するバラツキ」を表すものと言えます。そんなこと知ってるよ！という方も多いかと思いますが、以下では具体的な数値例をもとに、「説明変数と誤差項に相関がある」という現象がどう生じるかをのんびりと眺めていきます。

数値例で考える：手始めとして内生性がないケースについて

用いるデータの説明（ $n=1000$ ）

1000人についてのデータを考えます。 $Y$ が興味のある目的変数で、 $X$ が興味のある処理変数とします。本記事では基本的に、「 $X→Y$ の介入（因果）効果」の推定を目的として考えていきます。また、 $X$ と $Y$ 以外の要因（いわゆる共変量）として変数 $A, B, C, D, E$ を考えます。個人 $i$ がもつ各変数の値は、それぞれ $y_{i}, x_{i},a_{i}, b_{i}, c_{i}, d_{i}, e_{i}$ と表記します（ $i = 1, …, 1000$ ）。

具体的なデータの数値は以下になります（最初の10人分だけ示します）：

##            Y        X  A         B        C        D        E
## 1  117.74459 20.10945 50 17.515979 7.328762 5.274418 3.979622
## 2  101.26213 33.28693 50  4.512647 4.144204 4.805702 4.270394
## 3  104.58084 14.87584 50 14.527577 4.943072 5.706772 6.026504
## 4  132.57335 28.21539 50 20.072712 7.622195 6.590343 3.644171
## 5  119.69218 29.66154 50 14.602998 5.948058 4.876588 7.042868
## 6  131.00739 42.60949 50 13.724355 6.274851 4.674336 3.872113
## 7  135.54970 34.28185 50 18.904753 9.574860 3.883485 5.684925
## 8  123.86800 23.30899 50 21.037063 3.268138 5.216748 4.176329
## 9  117.50302 38.75542 50 10.460737 3.967846 3.858279 6.439549
## 10  96.44099 21.65111 50  7.983961 4.685668 4.136289 4.839025

ここで、このデータの $y_{i}$ は以下の式1によって完全に決定論的に作成されています。この式1は、本来は"神のみぞ知る"ような「 $Y$ の生成メカニズム」を表しているもの*4と考えてください。

$y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i}$ （式1）

つまりこのデータにおいては、個体のレベルで見たときの $y_{i}$ の値は「 $x_{i}, a_{i}, b_{i}, c_{i}, d_{i}$ の関数（ $y_{i} = f(x_{i}, a_{i}, b_{i}, c_{i}, d_{i})$ ）」として完全に決定論的に定まっています（上記の式1にはいわゆる”誤差項”がないことに注意してください）*5。

ここで、 ~~YOSHIKIとXの関係からForever Love~~ 与式1の関係から「 $x_{i}$ が1増加すると、 $y_{i}$ が1増加する関係にある」ことが分かります。つまり、「 $X→Y$ の介入効果（＝ $X$ を1単位増加させたときの $Y$ の増加量）」の"真の値"は、与式1から"1"となっています。

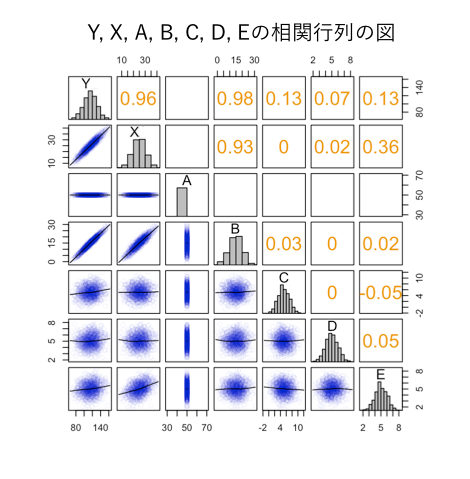
データ全体の概観をつかむために、 $Y, X, A, B, C, D$ の相関行列を図示してみます*6：

f:id:takehiko-i-hayashi:20170905064412p:plain

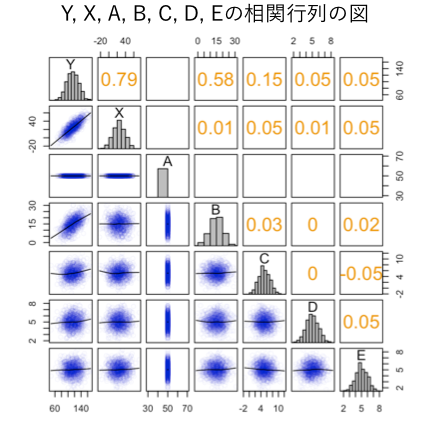
この図の中の右上部は相関係数（注： $p値$ と間違えやすいので注意）を、左下部は散布図を表しています。

このデータの特徴をまとめると以下のようになります：

データ内に含まれる変数は $Y$ と $X, A, B, C, D, E$
$A$ はサンプル内で常に $A=50$ であり、このデータにおいては分散を持たない変数となっている
$Y$ と $X, B, C$ の間には相関が見られる（YOSHIKI 1から生成されているので*7）
$X$ と $A, B, C, D, E$ は相関していない（注：これらのデータはRで作成しましたが、実際にプログラムコードの中でも $X, A, B, C, D, E$ は互いに独立に生成されています）

では、このような特徴をもつデータを用いて内生性と残差と誤差の関係についてのんびり眺めていきましょう。

のんびり回帰分析してみよう（まずは内生性がない場合）

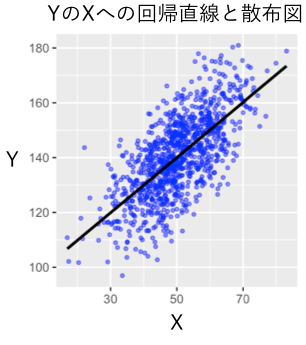
上記の数値表のデータにおいて、 $X$ と $Y$ のみが観察可能である（＝ $A, B, C, D, E$ の値は解析者には分からない）状況を想定し、 $X$ で $Y$ を単回帰してみます。回帰直線のプロットは以下のようになります：

f:id:takehiko-i-hayashi:20170906061338p:plain:w275

ここで $Y$ を $X$ で単回帰してみます。Rでの結果の要約は以下のようになります：

lm.res <- lm(Y ~ X)
summary(lm.res)
## 
## Call:
## lm(formula = Y ~ X)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -31.4218  -7.2333   0.0179   7.3268  31.5752 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 89.85904    0.66858  134.40   <2e-16 ***
## X            1.00607    0.02355   42.72   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.71 on 998 degrees of freedom
## Multiple R-squared:  0.6465, Adjusted R-squared:  0.6461 
## F-statistic:  1825 on 1 and 998 DF,  p-value: < 2.2e-16

ひとつづつ要素を確認してみましょう。

上記の"X"の行の”Estimate”が $X$ の回帰係数となります。回帰係数の推定値は「1.00607」となっています。回帰係数の正解の値はYOSHIKI 1より「1」なので、かなり高い精度で推定されているといえます。また、R2乗値（”R-squared”）は0.65、回帰分析の定数項（”Intercept”）は89.86になっています。

では、この回帰分析の~~「部屋」と「Yシャツ」と「私」~~「残差」と「誤差」と「 $X$ 」のあいだに相関があるか見ていきましょう。

「残差」と $X$ の相関をみてみよう（内生性がない場合）

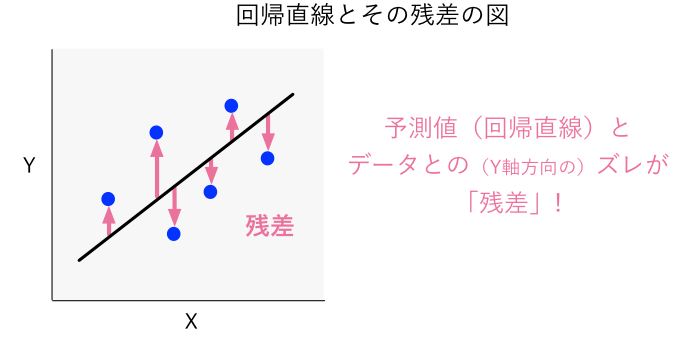
まず説明変数である $X$ と「残差」の相関を見てみます。残差とは「実際のデータである $y_{i}$ の値」と「得られた回帰モデルによる $y_{i}$ の予測値」の差分となります。図で表すと、実際のデータと回帰直線との縦側のズレが回帰分析における「残差」になります（下図のイメージ）。

f:id:takehiko-i-hayashi:20170907064804p:plain

数値的なイメージを掴むため、 $Y, X, Y$ の予測値（"Y_predict"）, 残差（"Y_residual"）の数値も以下に示しておきます（最初の10データ）：

##            Y         X Y_predict    Y_residual
## 1  117.74459 20.109453 110.09058   7.654013021
## 2  101.26213 33.286928 123.34805 -22.085923505
## 3  104.58084 14.875842 104.82519  -0.244353842
## 4  132.57335 28.215392 118.24573  14.327627596
## 5  119.69218 29.661538 119.70065  -0.008472325
## 6  131.00739 42.609494 132.72721  -1.719821246
## 7  135.54970 34.281848 124.34901  11.200687438
## 8  123.86800 23.308985 113.30953  10.558463946
## 9  117.50302 38.755424 128.84975 -11.346723721 
## 10  96.44099 21.651110 111.64159 -15.200605708

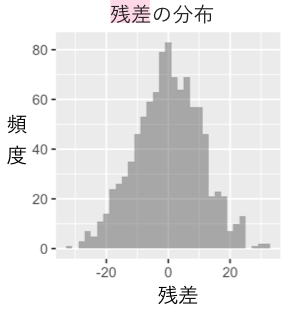
上記の「残差」の値の1000人分の分布も描いてみます。0の周りにおおむね対称にバラついていることが分かります。

f:id:takehiko-i-hayashi:20170908065042p:plain:w275

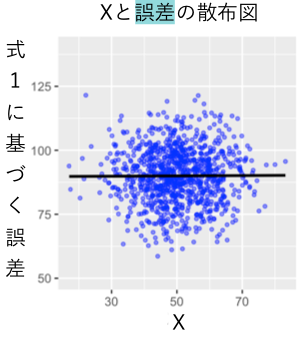
では「 $X$ 」と「残差」の相関を見てみましょう。どん！

f:id:takehiko-i-hayashi:20170908065231p:plain:w275

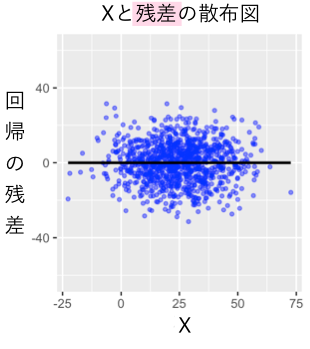
はい。安心してください。相関はありません。

これはある意味当たり前の話になります。なぜなら、そもそもこのような回帰分析では回帰直線の傾きが「説明変数以外で説明できないバラツキ」との相関がゼロになる（直交する）ように選ばれているからです（以下の参考図のイメージ／必要に応じて拡大などしていただければ幸いです）。

f:id:takehiko-i-hayashi:20170908065321p:plain

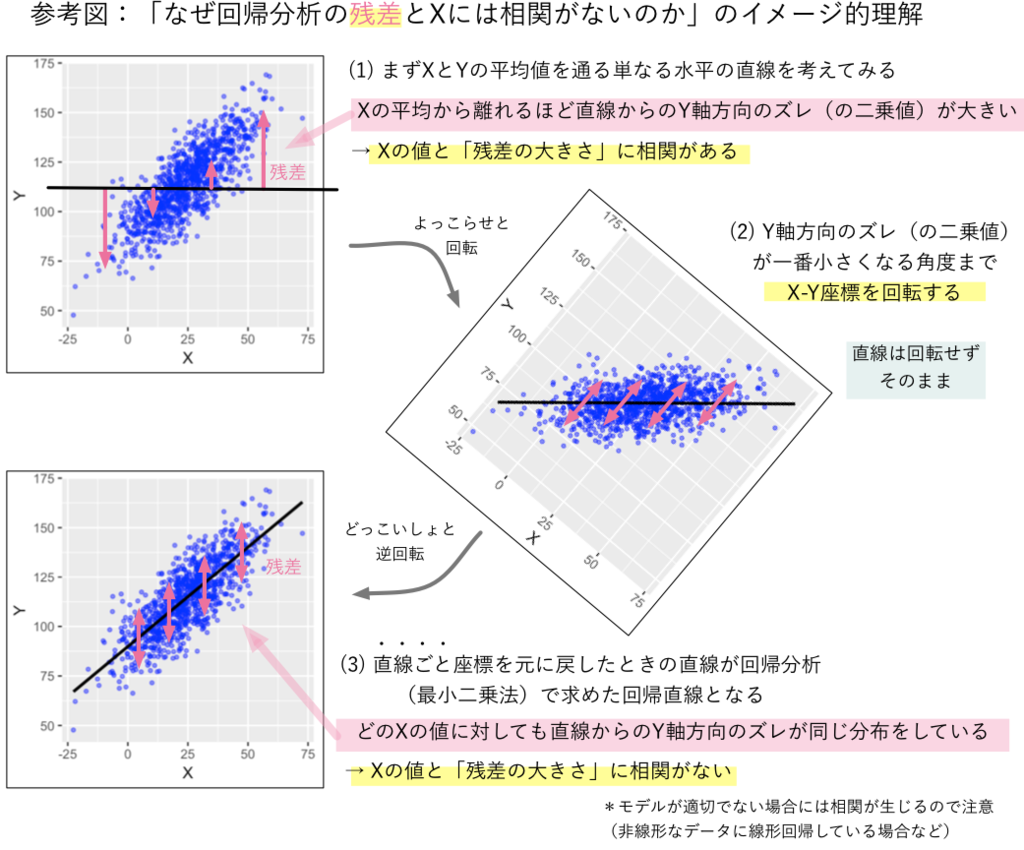
＊この辺りの回帰分析と残差にまつわるエトセトラについては以下のhoxo_mさんの記事の説明がとてもステキだと思いますので適宜絶賛ご参照いただければと思います：

・統計的消去で擬似相関を見抜こう！ - ほくそ笑む

「誤差」と「 $X$ 」の相関をみてみよう（内生性がない場合）

では次は、「誤差」と「 $X$ 」の相関をみていきましょう。

はてと。実は、困ったことに、通常はデータから「回帰分析の誤差項」そのものは算出できません。

・参考：BellCurveさんの良記事→ 27-3. 予測値と残差 | 統計学の時間 | 統計WEB

しかし、今回はチート的状況として「真のメカニズムモデル」が以下の式1により与えられています。

$y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i}$ （式1）

そこで本記事では、式1の変形から「 $Y$ のうち $X$ では決まらない部分」を「誤差」と定義することにより：

$誤差_{i} = y_{i} - x_{i} = a_{i} + 2b_{i} + c_{i} + d_{i}$

の式により「誤差」の値を算出していきます。

イメージを掴むため、 $Y, X, Y$ の予測値（"Y_predict"）, 残差（"Y_residual"）, 誤差（"Y_error_byEq1"）の数値表を以下に示します（最初の10データ）：

##            Y         X Y_predict    Y_residual Y_error_byEq1
## 1  117.74459 20.109453 110.09058   7.654013021      97.63514
## 2  101.26213 33.286928 123.34805 -22.085923505      67.97520
## 3  104.58084 14.875842 104.82519  -0.244353842      89.70500
## 4  132.57335 28.215392 118.24573  14.327627596     104.35796
## 5  119.69218 29.661538 119.70065  -0.008472325      90.03064
## 6  131.00739 42.609494 132.72721  -1.719821246      88.39790
## 7  135.54970 34.281848 124.34901  11.200687438     101.26785
## 8  123.86800 23.308985 113.30953  10.558463946     100.55901
## 9  117.50302 38.755424 128.84975 -11.346723721      78.74760
## 10  96.44099 21.651110 111.64159 -15.200605708      74.78988

上記の「誤差」の値の1000人分の分布は以下のようになります。90くらいの値を平均として対称に分布していることが分かります。

f:id:takehiko-i-hayashi:20170910074146p:plain:w275

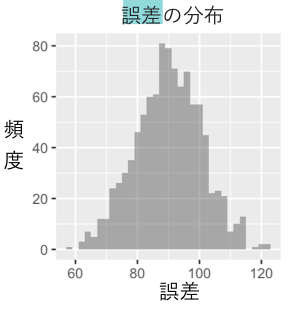
さて。ではこれらの誤差と $X$ のあいだに相関はあるでしょうか？誤差と $X$ の散布図を見てみましょう！

f:id:takehiko-i-hayashi:20170910074224p:plain:w275

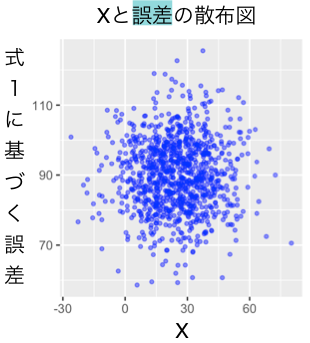
はい。相関はありません。つまりこの例では「内生性が」ない、ということになります。

ここで、「残差」と「誤差」の分布を重ねて見てみましょう。（改めて考えてみると、なかなか、「誤差の分布」と「残差の分布」を重ねてみることは無いのではないでしょうか。私も今回はじめてこのような作業をしてみました！）

f:id:takehiko-i-hayashi:20170910074247p:plain

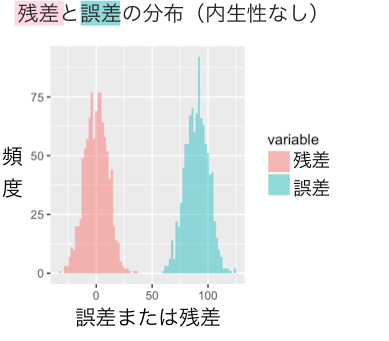
両者の分布は形状は似ていますが、平均の位置がズレています。この平均のズレの理由は、回帰分析の中では「 $X$ 以外の要因からの影響」のうち「平均に関する影響」は定数項（切片）として切り分けて扱われているためです。

上記の誤差について「誤差 - 回帰モデルの切片の値」として定数項分の補正を行うと、両者の分布の中心はゼロとなり、分布全体が以下のようにほぼ一致します：

f:id:takehiko-i-hayashi:20170910074306p:plain

はい。もしかしたら、このように切片のぶんだけ補正すれば「誤差」と「残差」の分布が重なるのは当たり前のようにも思う方も多いかもしれません*8。

しかしながら、後で見るように、「誤差」と「残差」の分布は（切片の補正を行っても）内生性がある場合には一般に重なりません。

少し脱線：（回帰分析の文脈における）「誤差」について改めておさらいをしてみる

さてさて。ここで少し「誤差」について、改めておさらいしてみたいと思います。（お急ぎの方はここの部分は読み飛ばしていただいても構いません）

今回の例では、私たちは与式1により「 $y_{i}$ の値は $x_{i}, a_{i}, b_{i}, c_{i}, d_{i}, e_{i}$ の値から決定論的に決まっている」ことを知っています。つまり、個体レベルで見ると $a_{i}, b_{i}, c_{i}, d_{i}, e_{i}$ からの寄与は「偶然」のものではありません。しかしながら、集団全体のレベルで回帰したときには、 $X$ の寄与としてカウントされない $a_{i}, b_{i}, c_{i}, d_{i}, e_{i}$ のバラツキからの寄与は、「誤差項」の中で表現されることになります。このように、回帰分析における「誤差項」というのは「偶然によるバラツキ」というよりも、「回帰モデル内で表現されていない要因に起因するバラツキ」と呼ぶべきものになっています。

ここでもう少し粘っこく考えてみると、１段階さらに遡って、 $a_{i}, b_{i}, c_{i}, d_{i}, e_{i}$ の値がもし「偶然により生じている」のであれば、それならばやはり「誤差項」は「偶然のバラツキ」と呼びうるのではないか、と考えることも可能かもしれません。この論理をどんどん敷衍していくと、そもそも「偶然とは何か」という哲学的な範疇の問いになってきます。本記事はひとまず、（人間は認知能力に限界があるので「偶然」という概念を都合よく用いたがるだけで）我々が現実の中で思考の対象とするようなマクロな現象は実際にはおおむね決定論的に定まっていると考えても差し支えないだろう、という立場で書いています。（とは言え、本記事の話の枠組みにおいては、例えば上記の $c_{i}$ の値のバラツキは本当は「神がサイコロを振ったことによる”真の偶然”によるバラツキなのだ！」と考えても、議論の大枠は全く変わりません）

ついでに、ちょっと本筋の話とは外れますが、また少し違う方向からも「誤差」について眺めてみましょう。誤差は「モデルに含まれていない要因に起因するもの」とは言っても、 $X→Y$ の単回帰モデル内に含まれていない $a_{i}, b_{i}, c_{i}, d_{i}, e_{i}$ からの寄与の全てが（ $X→Y$ の単回帰モデルの）「誤差項」の中で表現されているわけでもありません。集団の中でバラついていない部分による寄与は、「定数項」の中で表現されています。

例えば、今回の例では要因 $A$ には集団内でバラツキがないため、要因 $A$ の $Y$ の値への寄与は定数項の中でのみ表現されます。ここで注意してほしいのは、実際には、 $Y$ の値が構成される上で、要因Aは諸要因の中でもっとも寄与が大きい要因であることです。以下に式1ともともとのデータの数値表（最初の10データ）を再掲します：

式1は以下で：

$y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i}$ （式1）

データの数値は以下です：

##            Y        X  A         B        C        D        E
## 1  117.74459 20.10945 50 17.515979 7.328762 5.274418 3.979622
## 2  101.26213 33.28693 50  4.512647 4.144204 4.805702 4.270394
## 3  104.58084 14.87584 50 14.527577 4.943072 5.706772 6.026504
## 4  132.57335 28.21539 50 20.072712 7.622195 6.590343 3.644171
## 5  119.69218 29.66154 50 14.602998 5.948058 4.876588 7.042868
## 6  131.00739 42.60949 50 13.724355 6.274851 4.674336 3.872113
## 7  135.54970 34.28185 50 18.904753 9.574860 3.883485 5.684925
## 8  123.86800 23.30899 50 21.037063 3.268138 5.216748 4.176329
## 9  117.50302 38.75542 50 10.460737 3.967846 3.858279 6.439549
## 10  96.44099 21.65111 50  7.983961 4.685668 4.136289 4.839025

ここで、 $y_{i}$ の平均は105ですが、 $Y$ の値のほぼ半分となる50の分は要因 $A$ の寄与によるものです。しかしながら、ここでもし要因 $A$ を回帰モデルに加えても、「要因 $A$ は $Y$ に全く影響を及ぼさないもの」として解釈されます（集団内でバラツキがないので！）。

これは「メカニズム的な観点から見た $Y$ への寄与（ $Y$ の値の半分は $A$ による）」と「統計的に得られた回帰モデルの観点から見た $Y$ への寄与（ $Y$ は $A$ によらない）」は全く異なることを意味しています。（唐突に感じられるかもしれませんが、集団遺伝学的観点から見える「遺伝子の寄与」と、遺伝子ノックアウト法の観点から見える「遺伝子の寄与」が全く異なることと同型の論理です）

この違いを理解しておくことは、「統計的に得られた回帰モデル」の一般化可能性／外的妥当性を考える上で非常に重要なことです。もし、 $A$ の値が異なったり、 $A$ のバラツキが大きい集団に対して、上の数値例から得られた回帰式を用いて予測を行うと、全く的外れな予測をもたらす可能性があります。例えば、 $A=0$ の集団に対して上の数値例から得られた回帰式で予測を行なっても当然、 $Y$ の値は50の分だけズレてきます。また、 $A$ に大幅なバラツキのある集団に対して予測を行なっても、その $Y$ の予測能力は $A$ のバラツキの分だけ大幅に低下することになります。さらに、 $A$ が不均一な集団において、 $A$ と $X$ に交互作用があったり、 $A$ と $X$ の間にバックドアパス（参照）があったりする場合には、 $X$ への介入効果の推定にもズレが生じてきます。このように、均一性の高い集団に対する統計解析から得られたモデルからの結果を、その特性が異なる・不均一である集団に適応するときにはかなりの慎重さ（"humility"）が必要となります。

とても当たり前のことを言っているようですが、いざデータから回帰式を得てしまうと、それがあたかも普遍法則であるかのように捉えてしまいがちなのは人のロマンシング・サガとも言えるので、みんなで気をつけていきましょう。

いよいよ本題：「内生性がある場合」を眺めてみよう！

さてさてさてさて。少し脱線しました。本題に戻りましょう。いよいよ「内生性がある」場合を見ていきます。

今までの例とほぼ同じですが、その生成モデルにおいて $X$ が他の変数 $B$ と $E$ の関数である点だけ異なる場合を考えていきます。

$x_{i} = 2b_{i} + e_{i}$
$y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i}$ （式1）

このように、（モデルを構造方程式で表現したときに） $X$ 自体が他の変数の関数として左辺に現れているとき、 $X$ を内生変数と呼ぶようです（この辺りの計量経済系の用語の定義にはあまり自信ないですが。参考：内生変数＠コトバンク）。

$Y$ を生成する式は今までの例と同一の与式1です。大事なことなので繰り返しますが、目的変数である $Y$ を生成する式は今までと同一の与式1です。今までの例と同様に、与式1より、 $X→Y$ の介入効果（＝ $X$ を1単位増加させたときの $Y$ の増加量）は「1」となります。後でまた触れますが、与式1の中で「 $Y$ も $X$ と同じく $B$ の関数」となっていることがここのキモです。

データ全体の概観を掴むために相関行列を見てみましょう：

f:id:takehiko-i-hayashi:20170917092212p:plain

このデータにおける変数 $A, B, C, D, E$ の値は最初の例のデータと同じ値を用いています。一方、 $X$ の値は「 $X$ が $B$ と $E$ の関数」であるため $B$ と $E$ から新たに（決定論的に）生成された値になっており、（最初の例とは異なり） $X$ と $B$ , $X$ と $E$ の間に相関がみられています。

では、 $X$ と $Y$ のみが観察可能である状況を想定し、 $X$ で $Y$ を単回帰してみます。回帰直線のプロットは以下のようになります：

f:id:takehiko-i-hayashi:20170915062443p:plain:w275

はい。今回の例でも $Y$ の生成モデルとなる与式1は同じであるため、予想通り強い比例関係が見られています。

Rでの分析結果の要約は以下のようになります：

lm.res2 <- lm(Y2 ~ X2)
summary(lm.res2)

Call:
lm(formula = Y2 ~ X2)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.9827  -2.8054  -0.1508   2.9443  14.4078 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 46.70968    0.68146   68.54   <2e-16 ***
X2           2.74318    0.02649  103.57   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.537 on 998 degrees of freedom
Multiple R-squared:  0.9149, Adjusted R-squared:  0.9148 
F-statistic: 1.073e+04 on 1 and 998 DF,  p-value: < 2.2e-16

得られているR2乗値（"R-squared"）は「0.91」であり、一般論として適合したモデルはデータにおけるバラツキをかなり良く説明していると言えます。その一方で、 $X$ の介入効果の「真の値」は与式1より「1」であるにもかかわらず、得られた $X$ の回帰係数（"Estimate"）は「2.74」とその真の介入効果からは2.7倍もかさ増しされた数値になっています。（ちなみに回帰係数の推定値の標準誤差自体は0.025と小さく数値上の推定精度はかなり高くなっています）

このように、回帰モデル全体としての適合が良好であることと、その回帰モデルが介入効果の適切な推定値をもたらすことは本質的には別の問題となります。げに恐ろしきは内生性（a.k.a. 交絡）です。【20170928追記：サンプルサイズと一致性と内生性と多重共線性の関係については次のスライドの108枚目からをご参照いただければと思います→『バックドア基準の入門』＠統数研研究集会】

さて。いよいよ、このケースで~~「恋しさ」と「せつなさ」と「心強さ」~~「残差」と「誤差」と「 $X$ 」のあいだに相関があるかどうかを見てみましょう！

まず、 $X$ と「残差」のプロットを以下に示します：

f:id:takehiko-i-hayashi:20170917140546p:plain:w275

「 $X$ と残差」の間には相関はありません。（先ほども述べましたが、回帰直線の傾きは残差と $X$ の間に相関がないように選ばれているので、そもそもそういうものなのです）

一方、与式1から算出した「誤差」と、 $X$ の相関を見てみましょう。

f:id:takehiko-i-hayashi:20170917140720p:plain:w275

内生性、かくにん！ 「 $X$ と誤差」のプロットには明瞭な相関がみられました。

さて。この相関はなぜ生じているのでしょうか？ここでの「 $X$ と誤差」の相関は、以下のように両者がともに「 $B$ の関数」となっていることにより生じています。（以下にXの生成モデルと誤差の算出式を再掲）

$x_{i} = 2b_{i} + e_{i}$
$誤差_{i} = y_{i} - x_{i} = a_{i} + 2b_{i} + c_{i} + d_{i}$

このように、説明変数と誤差が同じ要因（この例では $B$ ）により影響を受けるとき*9に両者の間には相関が生じます。

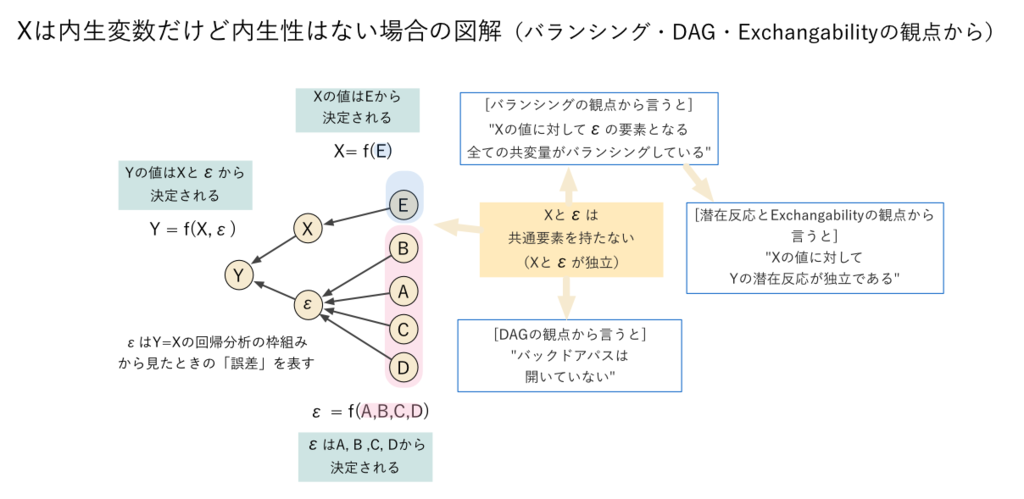
少し別の言い方をすると、（データ生成メカニズムの観点から見たときに）「誤差項に影響を与える要因の集合（ $A, B, C, D$ ）」と「 $X$ に与える要因の集合（ $B, E$ ）」に重複する部分があることによって内生性が生じている、とも言えます（下図／必要に応じて拡大などしていただければ幸いです）。【この状況については、Directed Acyclic Graph　(DAG)（参照：KRSK_phsさんによる良解説記事）の観点から言うと「 $X$ と $Y$ の間に閉じていないバックドアパスがある」、共変量のバランシングの観点から言うと「 $Y$ を決定する要因である $B$ の値が $X$ の値に対してバランシングしていない」、潜在反応モデルとExchangabilityの観点からは「 $X$ の値に対して $Y$ の潜在反応が非独立である」ことにより内生性が生じている、という説明の仕方がそれぞれできます。みなさま方におかれましては適宜お好みの説明の仕方をご採用いただければと思います！】

f:id:takehiko-i-hayashi:20170922063103p:plain

$X$ と「誤差」が同じものを含んでいるならば、その間に相関が生じるのは直感的にも理解しやすいですよね。このように、「誤差」をモデルに含まれていない諸変数の関数として（敢えて決定論的な枠組みを用いて）眺めてみると、少し「説明変数と誤差の相関」というものが直感的に捉えやすくなるかもしれません。

さて。では、この状況のときの「残差」と「誤差」の分布を眺めてみましょう。

以前にみた内生性がないケースでは「残差」と「誤差」の分布はほぼ重なっていました。しかし、今回の内生性があるケースにおいては、回帰分析からの「残差（ピンク）」と与式1から求めた「誤差（水色）」の分布は以下のようにズレています：

f:id:takehiko-i-hayashi:20170918145217p:plain:w400

上記の誤差について「誤差 - 回帰モデルの切片の値」として定数項分の補正を行ってみると以下の図のようになります。

f:id:takehiko-i-hayashi:20170918145436p:plain:w400

前回の内生性がないケースとは異なり、今回の内生性があるケースでは、残差と誤差の分布は重なりません。

また、ここで両者の分散に着目してみましょう。「残差」の分布のほうが分散が小さくなっています。これは、 $X$ がその生成メカニズムにおいて $B$ の成分を含んでいるため、本来は与式1内の $B$ の直接的な影響により生じている「 $Y$ のバラツキ」の一部が、 $X$ によって”過剰”に説明されている*10ために生じています。その $X$ による”過剰説明”によって、生成メカニズムから算出されている「誤差」の分散よりも、統計学的に得られた回帰モデルにおける「残差」の分散の方が小さくなっているわけです。

平均の違いに着目しても同じような「 $X$ による過剰説明」が生じています。本来は与式1内の $B$ によって決まる「平均の差」の一部が、 $X$ によっても「過剰に説明」されてしまっているため、回帰モデルからの定数項（切片分）で補正を行っても、両者の分布の平均も依然ズレるいます。

以上のことはつまり、内生性がないときには統計的に得られた回帰モデルからの残差は「真の誤差（モデル内の説明変数以外による影響の総体）」を反映していると期待できるものの、その一方で、内生性があるときにはそれらの「残差」と「真の誤差」もズレるということになります。

問い：“内生変数”があれば必ず内生性が生じる？

さて。ここで素朴な疑問を考えてみましょう。 $X$ が「内生変数」である場合には、必ず「内生性」が生じるのでしょうか？

試しに「 $X$ が $E$ のみの関数」である場合を見ていきましょう。この場合にも $X$ は「内生変数」と言えます*11。

$x_{i} = 10e_{i}$
$y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i}$ （式1）

$Y$ を生成する式は今までの例と同一の与式1です。今回は $X$ は $E$ のみの関数となっており、 $Y$ を生成する式にはEは含まれていないことに注意してください。

このデータに対してYをXで回帰した回帰分析は以下のようになります。

f:id:takehiko-i-hayashi:20170918151915p:plain:w275

lm.res3 <- lm(Y3 ~ X3)
summary(lm.res3)
## 
## Call:
## lm(formula = Y3 ~ X3)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -31.356  -7.180   0.016   7.369  31.698 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 89.68687    1.73408   51.72   <2e-16 ***
## X3           1.00638    0.03383   29.75   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.71 on 998 degrees of freedom
## Multiple R-squared:   0.47,  Adjusted R-squared:  0.4695 
## F-statistic:   885 on 1 and 998 DF,  p-value: < 2.2e-16

$X$ の回帰係数（”Estimate”）の正解は予式1より「1」ですが、 $n=1000$ とサンプルサイズも十分にあるので「1.00638」と高い精度で推定されています。つまり、 $X$ は内生変数ですが、今回のケースではバイアスは生じていません。

$X$ と「誤差」の相関をみてみましょう。

f:id:takehiko-i-hayashi:20170918152117p:plain:w275

この場合には、 $X$ と「誤差」の間には相関はありません。（ここには示しませんが、最初の「内生性がないケース」と同様に、「残差」と平均値を補正した「誤差」の分布も重なります）

上記の例が示すように、ややこしいですが、内生性が生じる上では「 $X$ が内生変数であること（システムを表す方程式の内部で決定されていること）」自体が本質的な要因であるわけではありません*12。

より本質的なのは、「 $X$ 」と「誤差項」を決定する要因の中に共通ものがあるかどうかということになるわけです（下図／必要に応じて拡大などしていただければ幸いです）*13。

f:id:takehiko-i-hayashi:20170923073737p:plain

（やっと）まとめ

はい。今回もとても長くなってしまいました。いちおう所感をまとめておきます：

内生性がないときは「誤差」と「残差」の分布は基本的に重なる（と期待できる）が*14、内生性があるときは「誤差」と「残差」は一般に重ならない*15
回帰モデルが $R^2$ 値の観点から「良く適合している」ということと、そのモデルの説明変数の回帰係数がその「因果効果の良い推定値」かどうかは、本質的には別の問題である
説明変数 $X$ が内生性をもつとき、「 $X$ の回帰係数」と「 $X$ への介入効果の推定値」はズレる（バイアスが生じる）
説明変数 $X$ が内生変数であっても、内生性をもつとは限らない。やれやれ。村（略）
「誤差」をモデルに含まれていない諸要因の「関数」として敢えて決定論的な枠組みから眺めてみると、少し「説明変数と誤差の相関」というものが身近になるかも

けっきょくggplot2の使い方がやっぱり今ひとつ腑に落ちず自分の老いを感じた
ggplot2を使いこなすシャレオツな若者を見ると自分の老いを感じる
tidyverseを使いこなすシャレオツな若者を見ると自分の老いを感じる
Stanを使いこなすシャレオツな若者を見ると自分の老いを感じる
最近までPythonの読みを「フィソン」だと思っていたことは絶対に秘密
あと環ROYのことも「かんろい」だと思ってた

はい。

本当は、これからさらに：

では、説明変数と残差に相関が出るのはどういうときなのか
「説明変数と誤差の相関」と「共変量のバランシング」の関係

などについてものんびり眺めてみようと思っていたのですが、もう力尽きたので、ここに書くのはやめておきます。

というわけで今回の記事は終わりです。
今回も非常に長い記事をここまでお読みいただいた方、大変ありがとうございました！

＃わたくしごとですが、来る10月1日から、弊研究所内でのルーティン的異動により所内企画部に半年間の時限付き出向となるため、暫くのあいだブログやSNSの稼働率はさらに大幅に低下すると思いますがどもすみません。

＃RStudioで書いた今回の「Rコード＋解説メモ」をこちらに置いておきますので、お好きな方は適宜どうぞ！→ html, Rmd

【参考情報など】

横浜国立大の黒木学先生による、因果関係を関数的関係の連なりとして捉える「構造的因果モデル」の教科書がさいきん出ました。いわゆるPearlの体系とRubinの体系が理論的にはシームレスであることも解説されています*16。この内容が日本語で読めることの幸せたるや！激オススメです！

構造的因果モデルの基礎

作者: 黒木学
出版社/メーカー: 共立出版
発売日: 2017/08/24
メディア: 単行本
この商品を含むブログを見る

黒木先生の本はちょとまだ難しいかな・・・という方は、こちらをどうぞ。わたくしと黒木先生の共著によるバックドア基準の入門的解説原稿も収録されています。

岩波データサイエンス Vol.3

作者: 岩波データサイエンス刊行委員会
出版社/メーカー: 岩波書店
発売日: 2016/06/10
メディア: 単行本（ソフトカバー）
この商品を含むブログ (4件) を見る

「因果効果を調べたい目的変数の挙動はそもそもどの共変量のどのような関数でありうるか」を粘り強く考える習慣や技量*17を身につけると、内生性に対する考察だけではなく、交互作用の理解や一般化可能性に関する考察もより明晰にできるようになっていきます。因果推論における交互作用の解説については、以下のKRSK_phsさんの記事が激オススメです。とても大事なことが分かりやすく説明されています！
krsk-phs.hatenablog.com

おまけ：たまきろい*18。ことの次第。ことばの因果的連関。凄い。

環ROY / ことの次第

*1:個人的には、ここの「信頼されるものとはなりえない」という全称的-ゼロイチ的な記述は強すぎるように感じます。一致推定量からのズレも実務上は「程度問題」だったりするので（構造的因果モデル的に言うとバックドアパスにも太いのと細いのがあるっていう話）、感度分析でもしてもう少し粘り強く「どれくらい信頼できるか」を考える方向を尊重してほしいように思ったりするところです

*2:わたくしの中での村上春樹のイメージは『世界の終わりとハードボイルド・ワンダーランド』くらいで止まっておりますが申し訳ありません

*3:誤差そのものは「差」を表す表現ですが、個々のデータにおける「誤差」ではなくデータ全体に含まれる「差の総体」を議論の対象とする場合には、「誤差」は実質的に「バラツキ」を指すと考えられるため、ここでは「偶然により生じるバラツキ」という表現を用いています

*4:つまり、単なる等式ではなく、生成メカニズムの表現としての構造方程式である

*5:ここで式1をYの式ではなく $y_{i}$ の式として記述しているのは、誤差項がなく完全に決定論的に定まっていることを強調することを意図しました。ここはどう書くかちょっと迷いました

*6:この相関行列の作成に関しては http://statmodeling.hatenablog.com/entry/scatter-plot-matrix のコードを参考にさせていただきました。多謝でございます

*7:式1の上ではYはDの関数でもあるのですが、データ上では明瞭には見えてないですね。Dの分散が小さいからかもしれません

*8:あるいは、回帰分析において両者の分布は「ぜひとも一致しておいてくれないと本当は色々と困るという事情により一致するのが当たり前だという期待が広く共有されているかもしれません」と記述した方がもしかしたら事態の正確な記述に近いのかもしれません

*9:構造的因果モデル的にいうとXとYの間のバックドアパスが閉じていないとき

*10:介入効果の推定の観点からは”過剰”という意味です。単なる予測モデルとしての観点からは特に問題はありません

*11:以前にも述べましたが、本稿では（モデルを構造方程式で表現したときに） $X$ 自体が他の変数の関数となっているとき、 $X$ を内生変数と呼びます

*12:というか内生変数の議論における「システム」の境界って誰が決めるんですかね？構造的因果モデルの観点から見ると、d分離によって議論すべき「システム」の境界はDAGの構造から理論的に定まりうるのだけれど

*13:構造的因果モデルの用語を用いてより正確に述べると「閉じていないバックドアパスがあるかどうか」

*14:「誤差」の定義にもよるかもしれない

*15:偶然に重なることはあるかもだけど

*16:潜在反応モデルの構造的因果モデルの枠組みによる定式化の解説など

*17:変数間の関数関係のグラフィカルな表現がDAGとなります

*18:今年のつくばロックフェスでライブを観ました。ものすごくかっこよかった！！！

Take a Risk：林岳彦の研究メモ

自らの研究に関連するエトセトラについてのメモ的ブログです。主にリスク学と統計学を扱っています。

内生性・交絡 revisited：説明変数と残差と誤差の相関をのんびり眺めるの巻

まずそもそも：回帰分析の「誤差項」って何だろう？

数値例で考える：手始めとして内生性がないケースについて

用いるデータの説明（ $n=1000$ ）

のんびり回帰分析してみよう（まずは内生性がない場合）

「残差」と $X$ の相関をみてみよう（内生性がない場合）

「誤差」と「 $X$ 」の相関をみてみよう（内生性がない場合）

少し脱線：（回帰分析の文脈における）「誤差」について改めておさらいをしてみる

いよいよ本題：「内生性がある場合」を眺めてみよう！

問い：“内生変数”があれば必ず内生性が生じる？

（やっと）まとめ

【参考情報など】

まずそもそも：回帰分析の「誤差項」って何だろう？

数値例で考える：手始めとして内生性がないケースについて

用いるデータの説明（）

のんびり回帰分析してみよう（まずは内生性がない場合）

「残差」との相関をみてみよう（内生性がない場合）

「誤差」と「」の相関をみてみよう（内生性がない場合）

少し脱線：（回帰分析の文脈における）「誤差」について改めておさらいをしてみる

いよいよ本題：「内生性がある場合」を眺めてみよう！

問い：“内生変数”があれば必ず内生性が生じる？

（やっと）まとめ

【参考情報など】

用いるデータの説明（ $n=1000$ ）

「残差」と $X$ の相関をみてみよう（内生性がない場合）

「誤差」と「 $X$ 」の相関をみてみよう（内生性がない場合）