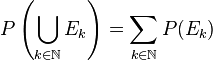Take a Risk：林岳彦の研究メモ

自らの研究に関連するエトセトラについてのメモ的ブログです。主にリスク学と統計学を扱っています。

トップ > リスク

内生性・交絡 revisited：説明変数と残差と誤差の相関をのんびり眺めるの巻

統計 リスク

こんにちは。林岳彦です。ggplot2を使いこなすシャレオツな若い人を見ると自分の老いを感じる今日このごろです。



さて。


今回は、「説明変数と誤差項に相関がある」とはどういうことか、について見ていきたいと思います。


経済学系の統計解析の本を読んでいると「内生性」という概念がよく出てきます（経済学系でない分野においては、「交絡」と呼ばれるものに実務上はおおむね対応する概念と言えます）。

この「内生性」の説明としては、例えば：

計量経済モデルにおいて、説明変数と誤差項との間に相関があるときに、内生性（endogeneity）があるという。このとき、説明変数は内生的（endogenous）であることになる。説明変数が内生的であれば、推定されたパラメータは一致推定量ではなくなり、推定値は統計学的に信頼されるものとはなりえない。

のように説明されます（内生性 - Wikipediaより引用*1。強調は引用者による）。


お分かりになりましたでしょうか。


うーん。このように「説明変数と誤差項との間に相関があるとき」とペロっと言われても、それはいったい内実としてどういうことなのでしょうか？ ここはちょっと直感的には掴みづらいところがあります。説明変数と誤差項との相関。やれやれ。村上春樹の小説の主人公ならばそう呟くところかと思われます*2。


少なくとも、私も長らくのあいだ「頭では概念として理解はできるけども、なんか腑に落ちた気がしないんだよなあ！」みたいなかんじでモヤモヤを抱えてきました。（一般的な傾向として、「交絡」の概念の方により親しんでいる人々にとっては「内生性」の概念はにわかに掴みづらいところがあると思います）

なので今回、「説明変数と誤差項に相関がある」という現象について、具体的な数値例と数式と散布図などを行き来しながら一度のんびりと眺めてみようと思いました。


以下はその観察記録です。あと、私はRの作図用パッケージであるggplot2を余り使ったことがなかったのでその練習も兼ねております。なんか、ggplot2を使う若者が、眩しかったので。

いつもながらめちゃくちゃ長い記事となっておりますが誠に申し訳ありません（一二塁間を鋭く転がるゴロに対して菊池涼介が飛びつくイメージで土下座）。もしご興味のある方はあくまでごゆるりとご参照いただければと思います。


注：以下の内容では特に何か新奇なことが書いてあるわけではありませんが、例えばもしあなたが「内生性があるとき、説明変数と残差の間には相関はありますか？」と聞かれて即答できなかったり、即答できたとしてもその話と「誤差」と「残差」の関係についてモヤモヤが残るようであれば、以下の内容を読むことで何らかの気付きがあるかもしれません。

まずそもそも：回帰分析の「誤差項」って何だろう？


まずちょっと誤差項について「そもそも」的な話をしておきたいと思います。「説明変数と誤差項の間に相関がある」という話が直感的に飲み込みにくい理由のひとつは、「誤差」という語の一般的なイメージにあるように思います。

分野と文脈にもよるかもしれませんが、一般に「誤差」という語は「偶然により生じるバラツキ」という意味内容で用いられることが多いかと思います*3。

この「誤差＝偶然によるバラツキ」のイメージだと、「説明変数」と「誤差項」が相関する、と言われてもちょっと直感的には分かりにくいかもしれません。「偶然」なのに「相関」する、というのはちょっとモヤモヤしますよね。偶然と相関は別ではない、むしろその一部として存在するのだ。村上春（以下略）


実際には、回帰分析における「誤差項」というのは、「偶然によるバラツキ」というよりも「回帰モデル内に含まれていない要因に起因するバラツキ」を表すものと言えます。そんなこと知ってるよ！という方も多いかと思いますが、以下では具体的な数値例をもとに、「説明変数と誤差項に相関がある」という現象がどう生じるかをのんびりと眺めていきます。

数値例で考える：手始めとして内生性がないケースについて

用いるデータの説明（ n=1000）

1000人についてのデータを考えます。 Yが興味のある目的変数で、 Xが興味のある処理変数とします。本記事では基本的に、「 X→Yの介入（因果）効果」の推定を目的として考えていきます。また、 Xと Y以外の要因（いわゆる共変量）として変数 A, B, C, D, Eを考えます。個人 iがもつ各変数の値は、それぞれ y_{i}, x_{i},a_{i}, b_{i}, c_{i}, d_{i}, e_{i}と表記します（ i = 1, …, 1000）。

具体的なデータの数値は以下になります（最初の10人分だけ示します）：

##            Y        X  A         B        C        D        E
## 1  117.74459 20.10945 50 17.515979 7.328762 5.274418 3.979622
## 2  101.26213 33.28693 50  4.512647 4.144204 4.805702 4.270394
## 3  104.58084 14.87584 50 14.527577 4.943072 5.706772 6.026504
## 4  132.57335 28.21539 50 20.072712 7.622195 6.590343 3.644171
## 5  119.69218 29.66154 50 14.602998 5.948058 4.876588 7.042868
## 6  131.00739 42.60949 50 13.724355 6.274851 4.674336 3.872113
## 7  135.54970 34.28185 50 18.904753 9.574860 3.883485 5.684925
## 8  123.86800 23.30899 50 21.037063 3.268138 5.216748 4.176329
## 9  117.50302 38.75542 50 10.460737 3.967846 3.858279 6.439549
## 10  96.44099 21.65111 50  7.983961 4.685668 4.136289 4.839025

ここで、このデータの y_{i}は以下の式1によって完全に決定論的に作成されています。この式1は、本来は"神のみぞ知る"ような「 Yの生成メカニズム」を表しているもの*4と考えてください。

y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i} （式1）

つまりこのデータにおいては、個体のレベルで見たときの y_{i}の値は「 x_{i}, a_{i}, b_{i}, c_{i}, d_{i}の関数（ y_{i} = f(x_{i}, a_{i}, b_{i}, c_{i}, d_{i})）」として完全に決定論的に定まっています（上記の式1にはいわゆる”誤差項”がないことに注意してください）*5。

ここで、 YOSHIKIとXの関係からForever Love 与式1の関係から「 x_{i}が1増加すると、 y_{i}が1増加する関係にある」ことが分かります。つまり、「 X→Yの介入効果（＝ Xを1単位増加させたときの Yの増加量）」の"真の値"は、与式1から"1"となっています。

データ全体の概観をつかむために、 Y, X, A, B, C, Dの相関行列を図示してみます*6：


f:id:takehiko-i-hayashi:20170905064412p:plain

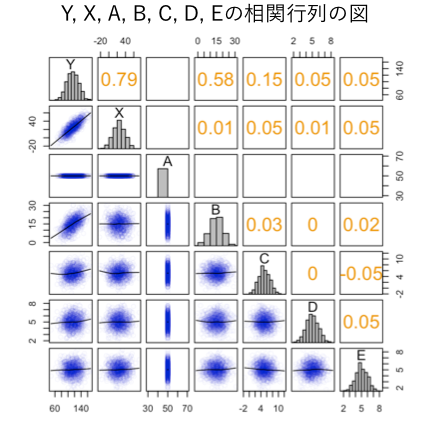
この図の中の右上部は相関係数（注： p値と間違えやすいので注意）を、左下部は散布図を表しています。

このデータの特徴をまとめると以下のようになります：

  • データ内に含まれる変数は Yと X, A, B, C, D, E
  • Aはサンプル内で常に A=50であり、このデータにおいては分散を持たない変数となっている
  • Yと X, B, Cの間には相関が見られる（YOSHIKI 1から生成されているので*7）
  • Xと A, B, C, D, Eは相関していない（注：これらのデータはRで作成しましたが、実際にプログラムコードの中でも X, A, B, C, D, Eは互いに独立に生成されています）

では、このような特徴をもつデータを用いて内生性と残差と誤差の関係についてのんびり眺めていきましょう。

のんびり回帰分析してみよう（まずは内生性がない場合）

上記の数値表のデータにおいて、 Xと Yのみが観察可能である（＝ A, B, C, D, Eの値は解析者には分からない）状況を想定し、 Xで Yを単回帰してみます。回帰直線のプロットは以下のようになります：


f:id:takehiko-i-hayashi:20170906061338p:plain:w275

ここで Yを Xで単回帰してみます。Rでの結果の要約は以下のようになります：

lm.res <- lm(Y ~ X)
summary(lm.res)
## 
## Call:
## lm(formula = Y ~ X)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -31.4218  -7.2333   0.0179   7.3268  31.5752 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 89.85904    0.66858  134.40   <2e-16 ***
## X            1.00607    0.02355   42.72   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.71 on 998 degrees of freedom
## Multiple R-squared:  0.6465, Adjusted R-squared:  0.6461 
## F-statistic:  1825 on 1 and 998 DF,  p-value: < 2.2e-16

ひとつづつ要素を確認してみましょう。

上記の"X"の行の”Estimate”が Xの回帰係数となります。回帰係数の推定値は「1.00607」となっています。回帰係数の正解の値はYOSHIKI 1より「1」なので、かなり高い精度で推定されているといえます。また、R2乗値（”R-squared”）は0.65、回帰分析の定数項（”Intercept”） は89.86になっています。


では、この回帰分析の「部屋」と「Yシャツ」と「私」「残差」と「誤差」と「 X」のあいだに相関があるか見ていきましょう。

「残差」と Xの相関をみてみよう（内生性がない場合）

まず説明変数である Xと「残差」の相関を見てみます。残差とは「実際のデータである y_{i}の値」と「得られた回帰モデルによる y_{i}の予測値」の差分となります。図で表すと、実際のデータと回帰直線との縦側のズレが回帰分析における「残差」になります（下図のイメージ）。


f:id:takehiko-i-hayashi:20170907064804p:plain

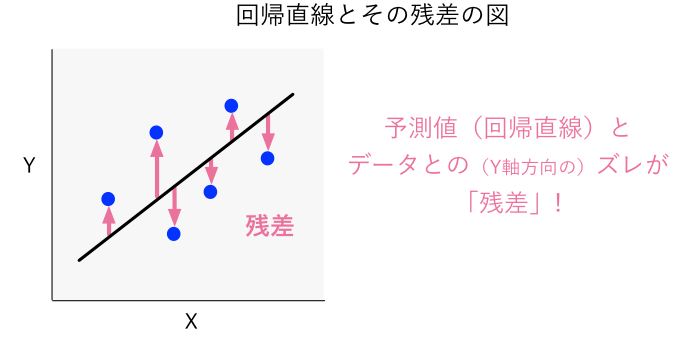
数値的なイメージを掴むため、 Y, X, Yの予測値（"Y_predict"）, 残差（"Y_residual"）の数値も以下に示しておきます（最初の10データ）：

##            Y         X Y_predict    Y_residual
## 1  117.74459 20.109453 110.09058   7.654013021
## 2  101.26213 33.286928 123.34805 -22.085923505
## 3  104.58084 14.875842 104.82519  -0.244353842
## 4  132.57335 28.215392 118.24573  14.327627596
## 5  119.69218 29.661538 119.70065  -0.008472325
## 6  131.00739 42.609494 132.72721  -1.719821246
## 7  135.54970 34.281848 124.34901  11.200687438
## 8  123.86800 23.308985 113.30953  10.558463946
## 9  117.50302 38.755424 128.84975 -11.346723721 
## 10  96.44099 21.651110 111.64159 -15.200605708

上記の「残差」の値の1000人分の分布も描いてみます。0の周りにおおむね対称にバラついていることが分かります。


f:id:takehiko-i-hayashi:20170908065042p:plain:w275

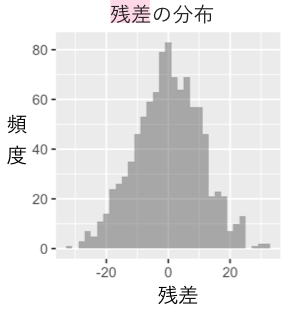
では「 X」と「残差」の相関を見てみましょう。どん！


f:id:takehiko-i-hayashi:20170908065231p:plain:w275

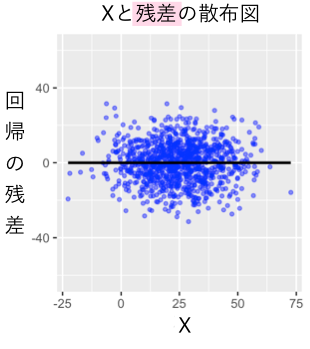
はい。安心してください。相関はありません。

これはある意味当たり前の話になります。なぜなら、そもそもこのような回帰分析では回帰直線の傾きが「説明変数以外で説明できないバラツキ」との相関がゼロになる（直交する）ように選ばれているからです（以下の参考図のイメージ／必要に応じて拡大などしていただければ幸いです）。


f:id:takehiko-i-hayashi:20170908065321p:plain


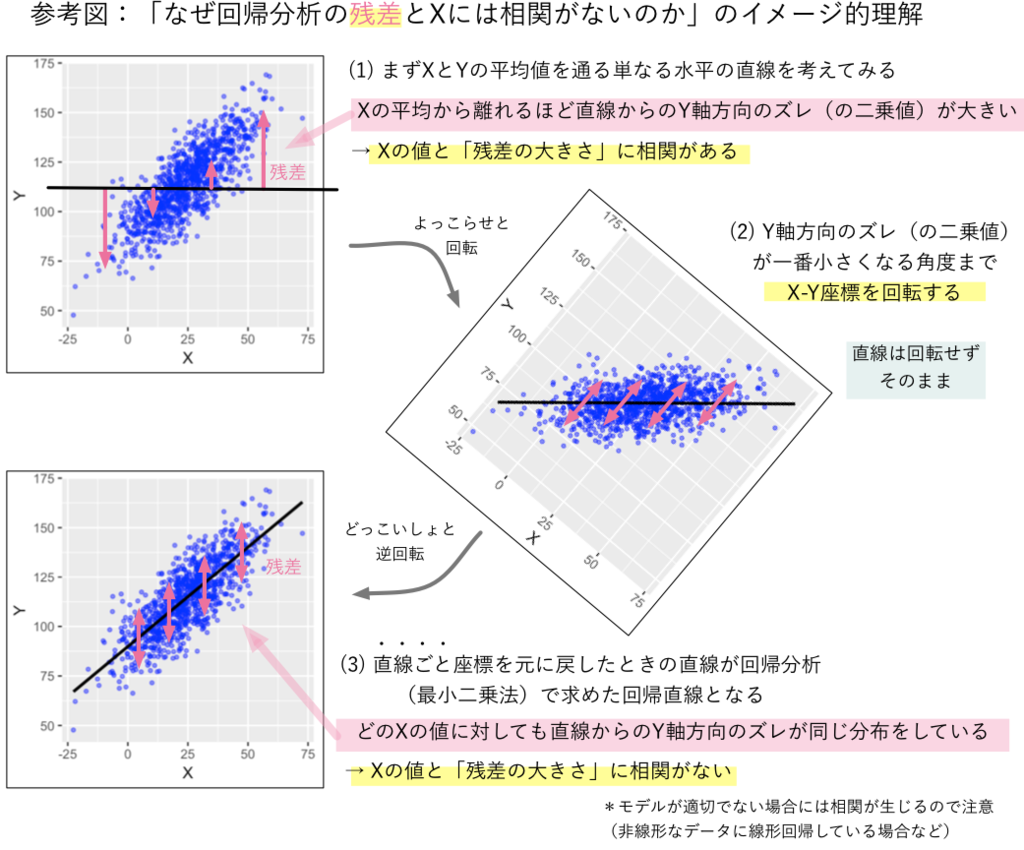
＊この辺りの回帰分析と残差にまつわるエトセトラについては以下のhoxo_mさんの記事の説明がとてもステキだと思いますので適宜絶賛ご参照いただければと思います：

・ 統計的消去で擬似相関を見抜こう！ - ほくそ笑む


「誤差」と「 X」の相関をみてみよう（内生性がない場合）

では次は、「誤差」と「 X」の相関をみていきましょう。

はてと。実は、困ったことに、通常はデータから「回帰分析の誤差項」そのものは算出できません。

・参考：BellCurveさんの良記事→ 27-3. 予測値と残差 | 統計学の時間 | 統計WEB

しかし、今回はチート的状況として「真のメカニズムモデル」が以下の式1により与えられています。

y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i} （式1）

そこで本記事では、式1の変形から「 Yのうち Xでは決まらない部分」を「誤差」と定義することにより：

誤差_{i} = y_{i} - x_{i} = a_{i} + 2b_{i} + c_{i} + d_{i}

の式により「誤差」の値を算出していきます。

イメージを掴むため、 Y, X, Yの予測値（"Y_predict"）, 残差（"Y_residual"）, 誤差（"Y_error_byEq1"）の数値表を以下に示します（最初の10データ）：

##            Y         X Y_predict    Y_residual Y_error_byEq1
## 1  117.74459 20.109453 110.09058   7.654013021      97.63514
## 2  101.26213 33.286928 123.34805 -22.085923505      67.97520
## 3  104.58084 14.875842 104.82519  -0.244353842      89.70500
## 4  132.57335 28.215392 118.24573  14.327627596     104.35796
## 5  119.69218 29.661538 119.70065  -0.008472325      90.03064
## 6  131.00739 42.609494 132.72721  -1.719821246      88.39790
## 7  135.54970 34.281848 124.34901  11.200687438     101.26785
## 8  123.86800 23.308985 113.30953  10.558463946     100.55901
## 9  117.50302 38.755424 128.84975 -11.346723721      78.74760
## 10  96.44099 21.651110 111.64159 -15.200605708      74.78988

上記の「誤差」の値の1000人分の分布は以下のようになります。90くらいの値を平均として対称に分布していることが分かります。


f:id:takehiko-i-hayashi:20170910074146p:plain:w275


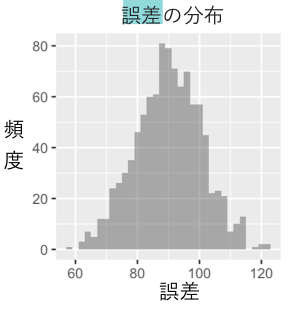
さて。ではこれらの誤差と Xのあいだに相関はあるでしょうか？ 誤差と Xの散布図を見てみましょう！


f:id:takehiko-i-hayashi:20170910074224p:plain:w275

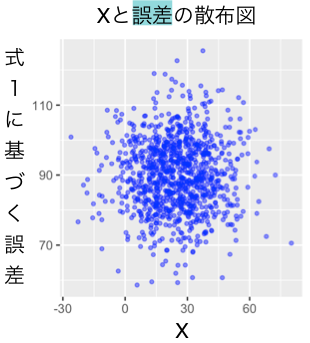
はい。相関はありません。つまりこの例では「内生性が」ない、ということになります。


ここで、「残差」と「誤差」の分布を重ねて見てみましょう。（改めて考えてみると、なかなか、「誤差の分布」と「残差の分布」を重ねてみることは無いのではないでしょうか。私も今回はじめてこのような作業をしてみました！）


f:id:takehiko-i-hayashi:20170910074247p:plain

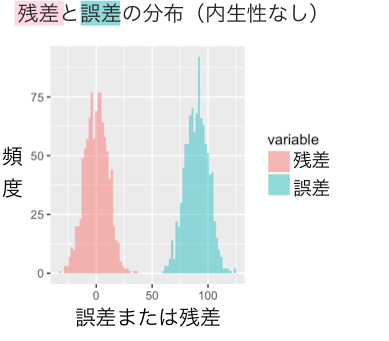
両者の分布は形状は似ていますが、平均の位置がズレています。この平均のズレの理由は、回帰分析の中では「 X以外の要因からの影響」のうち「平均に関する影響」は定数項（切片）として切り分けて扱われているためです。

上記の誤差について「誤差 - 回帰モデルの切片の値」として定数項分の補正を行うと、両者の分布の中心はゼロとなり、分布全体が以下のようにほぼ一致します：


f:id:takehiko-i-hayashi:20170910074306p:plain

はい。もしかしたら、このように切片のぶんだけ補正すれば「誤差」と「残差」の分布が重なるのは当たり前のようにも思う方も多いかもしれません*8。

しかしながら、後で見るように、「誤差」と「残差」の分布は（切片の補正を行っても）内生性がある場合には一般に重なりません。

少し脱線：（回帰分析の文脈における）「誤差」について改めておさらいをしてみる

さてさて。ここで少し「誤差」について、改めておさらいしてみたいと思います。（お急ぎの方はここの部分は読み飛ばしていただいても構いません）


今回の例では、私たちは与式1により「 y_{i}の値は x_{i}, a_{i}, b_{i}, c_{i}, d_{i}, e_{i}の値から決定論的に決まっている」ことを知っています。つまり、個体レベルで見ると a_{i}, b_{i}, c_{i}, d_{i}, e_{i}からの寄与は「偶然」のものではありません。しかしながら、集団全体のレベルで回帰したときには、 Xの寄与としてカウントされない a_{i}, b_{i}, c_{i}, d_{i}, e_{i}のバラツキからの寄与は、「誤差項」の中で表現されることになります。このように、回帰分析における「誤差項」というのは「偶然によるバラツキ」というよりも、「回帰モデル内で表現されていない要因に起因するバラツキ」と呼ぶべきものになっています。

ここでもう少し粘っこく考えてみると、１段階さらに遡って、 a_{i}, b_{i}, c_{i}, d_{i}, e_{i}の値がもし「偶然により生じている」のであれば、それならばやはり「誤差項」は「偶然のバラツキ」と呼びうるのではないか、と考えることも可能かもしれません。この論理をどんどん敷衍していくと、そもそも「偶然とは何か」という哲学的な範疇の問いになってきます。本記事はひとまず、（人間は認知能力に限界があるので「偶然」という概念を都合よく用いたがるだけで）我々が現実の中で思考の対象とするようなマクロな現象は実際にはおおむね決定論的に定まっていると考えても差し支えないだろう、という立場で書いています。（とは言え、本記事の話の枠組みにおいては、例えば上記の c_{i}の値のバラツキは本当は「神がサイコロを振ったことによる”真の偶然”によるバラツキなのだ！」と考えても、議論の大枠は全く変わりません）

ついでに、ちょっと本筋の話とは外れますが、また少し違う方向からも「誤差」について眺めてみましょう。誤差は「モデルに含まれていない要因に起因するもの」とは言っても、 X→Yの単回帰モデル内に含まれていない a_{i}, b_{i}, c_{i}, d_{i}, e_{i}からの寄与の全てが（ X→Yの単回帰モデルの）「誤差項」の中で表現されているわけでもありません。集団の中でバラついていない部分による寄与は、「定数項」の中で表現されています。

例えば、今回の例では要因 Aには集団内でバラツキがないため、要因 Aの Yの値への寄与は定数項の中でのみ表現されます。ここで注意してほしいのは、実際には、 Yの値が構成される上で、要因Aは諸要因の中でもっとも寄与が大きい要因であることです。以下に式1ともともとのデータの数値表（最初の10データ）を再掲します：

式1は以下で：

y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i} （式1）

データの数値は以下です：

##            Y        X  A         B        C        D        E
## 1  117.74459 20.10945 50 17.515979 7.328762 5.274418 3.979622
## 2  101.26213 33.28693 50  4.512647 4.144204 4.805702 4.270394
## 3  104.58084 14.87584 50 14.527577 4.943072 5.706772 6.026504
## 4  132.57335 28.21539 50 20.072712 7.622195 6.590343 3.644171
## 5  119.69218 29.66154 50 14.602998 5.948058 4.876588 7.042868
## 6  131.00739 42.60949 50 13.724355 6.274851 4.674336 3.872113
## 7  135.54970 34.28185 50 18.904753 9.574860 3.883485 5.684925
## 8  123.86800 23.30899 50 21.037063 3.268138 5.216748 4.176329
## 9  117.50302 38.75542 50 10.460737 3.967846 3.858279 6.439549
## 10  96.44099 21.65111 50  7.983961 4.685668 4.136289 4.839025

ここで、 y_{i}の平均は105ですが、 Yの値のほぼ半分となる50の分は要因 Aの寄与によるものです。しかしながら、ここでもし要因 Aを回帰モデルに加えても、「要因 Aは Yに全く影響を及ぼさないもの」として解釈されます（集団内でバラツキがないので！）。

これは「メカニズム的な観点から見た Yへの寄与（ Yの値の半分は Aによる）」と「統計的に得られた回帰モデルの観点から見た Yへの寄与（ Yは Aによらない）」は全く異なることを意味しています。（唐突に感じられるかもしれませんが、集団遺伝学的観点から見える「遺伝子の寄与」と、遺伝子ノックアウト法の観点から見える「遺伝子の寄与」が全く異なることと同型の論理です）

この違いを理解しておくことは、「統計的に得られた回帰モデル」の一般化可能性／外的妥当性を考える上で非常に重要なことです。もし、 Aの値が異なったり、 Aのバラツキが大きい集団に対して、上の数値例から得られた回帰式を用いて予測を行うと、全く的外れな予測をもたらす可能性があります。例えば、 A=0の集団に対して上の数値例から得られた回帰式で予測を行なっても当然、 Yの値は50の分だけズレてきます。また、 Aに大幅なバラツキのある集団に対して予測を行なっても、その Yの予測能力は Aのバラツキの分だけ大幅に低下することになります。さらに、 Aが不均一な集団において、 Aと Xに交互作用があったり、 Aと Xの間にバックドアパス（参照）があったりする場合には、 Xへの介入効果の推定にもズレが生じてきます。このように、均一性の高い集団に対する統計解析から得られたモデルからの結果を、その特性が異なる・不均一である集団に適応するときにはかなりの慎重さ（"humility"）が必要となります。


とても当たり前のことを言っているようですが、いざデータから回帰式を得てしまうと、それがあたかも普遍法則であるかのように捉えてしまいがちなのは人のロマンシング・サガとも言えるので、みんなで気をつけていきましょう。

いよいよ本題：「内生性がある場合」を眺めてみよう！

さてさてさてさて。少し脱線しました。本題に戻りましょう。いよいよ「内生性がある」場合を見ていきます。

今までの例とほぼ同じですが、その生成モデルにおいて Xが他の変数 Bと Eの関数である点だけ異なる場合を考えていきます。

x_{i} = 2b_{i} + e_{i}
y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i} （式1）

このように、（モデルを構造方程式で表現したときに） X自体が他の変数の関数として左辺に現れているとき、 Xを内生変数と呼ぶようです（この辺りの計量経済系の用語の定義にはあまり自信ないですが。参考：内生変数＠コトバンク）。

Yを生成する式は今までの例と同一の与式1です。大事なことなので繰り返しますが、目的変数である Yを生成する式は今までと同一の与式1です。今までの例と同様に、与式1より、 X→Yの介入効果（＝ Xを1単位増加させたときの Yの増加量）は「1」となります。後でまた触れますが、与式1の中で「 Yも Xと同じく Bの関数」となっていることがここのキモです。


データ全体の概観を掴むために相関行列を見てみましょう：


f:id:takehiko-i-hayashi:20170917092212p:plain

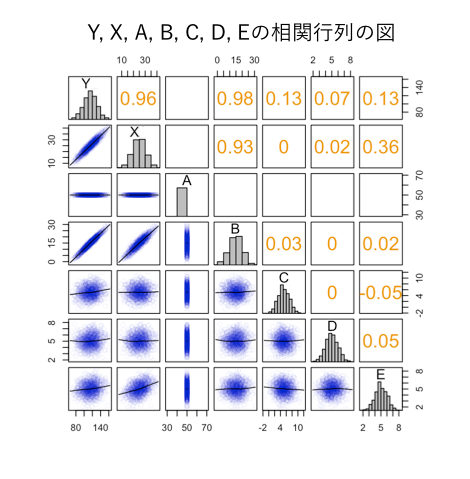
このデータにおける変数 A, B, C, D, Eの値は最初の例のデータと同じ値を用いています。一方、 Xの値は「 Xが Bと Eの関数」であるため Bと Eから新たに（決定論的に）生成された値になっており、（最初の例とは異なり） Xと B, Xと Eの間に相関がみられています。

では、 Xと Yのみが観察可能である状況を想定し、 Xで Yを単回帰してみます。回帰直線のプロットは以下のようになります：


f:id:takehiko-i-hayashi:20170915062443p:plain:w275

はい。今回の例でも Yの生成モデルとなる与式1は同じであるため、予想通り強い比例関係が見られています。

Rでの分析結果の要約は以下のようになります：

lm.res2 <- lm(Y2 ~ X2)
summary(lm.res2)

Call:
lm(formula = Y2 ~ X2)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.9827  -2.8054  -0.1508   2.9443  14.4078 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 46.70968    0.68146   68.54   <2e-16 ***
X2           2.74318    0.02649  103.57   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.537 on 998 degrees of freedom
Multiple R-squared:  0.9149, Adjusted R-squared:  0.9148 
F-statistic: 1.073e+04 on 1 and 998 DF,  p-value: < 2.2e-16

得られているR2乗値（"R-squared"）は「0.91」であり、一般論として適合したモデルはデータにおけるバラツキをかなり良く説明していると言えます。その一方で、 Xの介入効果の「真の値」は与式1より「1」であるにもかかわらず、得られた Xの回帰係数（"Estimate"）は「2.74」とその真の介入効果からは2.7倍もかさ増しされた数値になっています。（ちなみに回帰係数の推定値の標準誤差自体は0.025と小さく数値上の推定精度はかなり高くなっています）

このように、回帰モデル全体としての適合が良好であることと、その回帰モデルが介入効果の適切な推定値をもたらすことは本質的には別の問題となります。げに恐ろしきは内生性（a.k.a. 交絡）です。【20170928追記：サンプルサイズと一致性と内生性と多重共線性の関係については次のスライドの108枚目からをご参照いただければと思います→『バックドア基準の入門』＠統数研研究集会】



さて。いよいよ、このケースで「恋しさ」と「せつなさ」と「心強さ」「残差」と「誤差」と「 X」のあいだに相関があるかどうかを見てみましょう！

まず、 Xと「残差」のプロットを以下に示します：

f:id:takehiko-i-hayashi:20170917140546p:plain:w275

「 Xと残差」の間には相関はありません。（先ほども述べましたが、回帰直線の傾きは残差と Xの間に相関がないように選ばれているので、そもそもそういうものなのです）

一方、与式1から算出した「誤差」と、 Xの相関を見てみましょう。


f:id:takehiko-i-hayashi:20170917140720p:plain:w275

内生性、かくにん！ 「 Xと誤差」のプロットには明瞭な相関がみられました。

さて。この相関はなぜ生じているのでしょうか？ ここでの「 Xと誤差」の相関は、以下のように両者がともに「 Bの関数」となっていることにより生じています。（以下にXの生成モデルと誤差の算出式を再掲）

x_{i} = 2b_{i} + e_{i}
誤差_{i} = y_{i} - x_{i} = a_{i} + 2b_{i} + c_{i} + d_{i}

このように、説明変数と誤差が同じ要因（この例ではB）により影響を受けるとき*9に両者の間には相関が生じます。

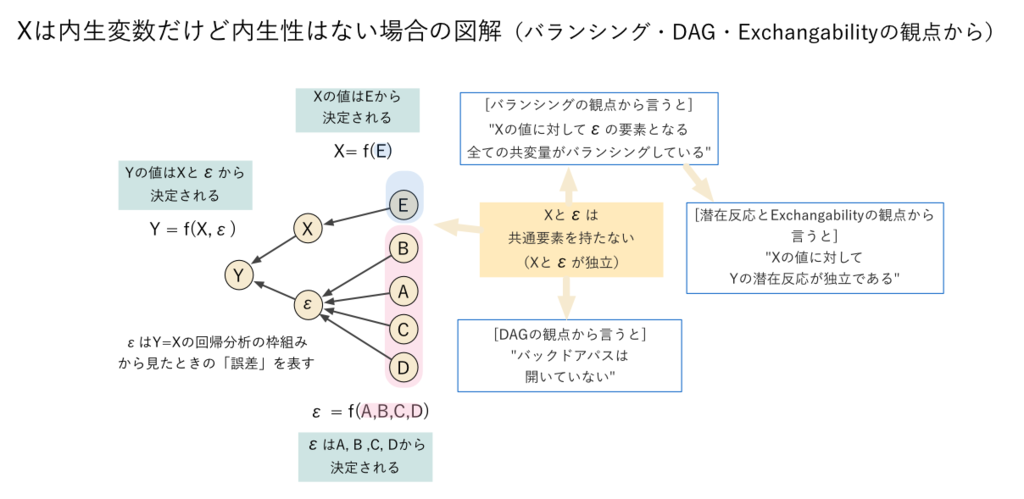
少し別の言い方をすると、（データ生成メカニズムの観点から見たときに）「誤差項に影響を与える要因の集合（A, B, C, D）」と「Xに与える要因の集合（B, E）」に重複する部分があることによって内生性が生じている、とも言えます（下図／必要に応じて拡大などしていただければ幸いです）。【この状況については、Directed Acyclic Graph　(DAG)（参照：KRSK_phsさんによる良解説記事）の観点から言うと「 Xと Yの間に閉じていないバックドアパスがある」、共変量のバランシングの観点から言うと「 Yを決定する要因である Bの値が Xの値に対してバランシングしていない」、潜在反応モデルとExchangabilityの観点からは「 Xの値に対して Yの潜在反応が非独立である」ことにより内生性が生じている、という説明の仕方がそれぞれできます。みなさま方におかれましては適宜お好みの説明の仕方をご採用いただければと思います！】


f:id:takehiko-i-hayashi:20170922063103p:plain

Xと「誤差」が同じものを含んでいるならば、その間に相関が生じるのは直感的にも理解しやすいですよね。このように、「誤差」をモデルに含まれていない諸変数の関数として（敢えて決定論的な枠組みを用いて）眺めてみると、少し「説明変数と誤差の相関」というものが直感的に捉えやすくなるかもしれません。


さて。では、この状況のときの「残差」と「誤差」の分布を眺めてみましょう。

以前にみた内生性がないケースでは「残差」と「誤差」の分布はほぼ重なっていました。しかし、今回の内生性があるケースにおいては、回帰分析からの「残差（ピンク）」と与式1から求めた「誤差（水色）」の分布は以下のようにズレています：


f:id:takehiko-i-hayashi:20170918145217p:plain:w400

上記の誤差について「誤差 - 回帰モデルの切片の値」として定数項分の補正を行ってみると以下の図のようになります。


f:id:takehiko-i-hayashi:20170918145436p:plain:w400

前回の内生性がないケースとは異なり、今回の内生性があるケースでは、残差と誤差の分布は重なりません。

また、ここで両者の分散に着目してみましょう。「残差」の分布のほうが分散が小さくなっています。これは、 Xがその生成メカニズムにおいて Bの成分を含んでいるため、本来は与式1内の Bの直接的な影響により生じている「 Yのバラツキ」の一部が、 Xによって”過剰”に説明されている*10ために生じています。その Xによる”過剰説明”によって、生成メカニズムから算出されている「誤差」の分散よりも、統計学的に得られた回帰モデルにおける「残差」の分散の方が小さくなっているわけです。

平均の違いに着目しても同じような「 Xによる過剰説明」が生じています。本来は与式1内の Bによって決まる「平均の差」の一部が、 Xによっても「過剰に説明」されてしまっているため、回帰モデルからの定数項（切片分）で補正を行っても、両者の分布の平均も依然ズレるいます。

以上のことはつまり、内生性がないときには統計的に得られた回帰モデルからの残差は「真の誤差（モデル内の説明変数以外による影響の総体）」を反映していると期待できるものの、その一方で、内生性があるときにはそれらの「残差」と「真の誤差」もズレるということになります。

問い：“内生変数”があれば必ず内生性が生じる？

さて。ここで素朴な疑問を考えてみましょう。 Xが「内生変数」である場合には、必ず「内生性」が生じるのでしょうか？

試しに「 Xが Eのみの関数」である場合を見ていきましょう。この場合にも Xは「内生変数」と言えます*11。

x_{i} = 10e_{i}
y_{i} = x_{i} + a_{i} + 2b_{i} + c_{i} + d_{i}（式1）

Yを生成する式は今までの例と同一の与式1です。今回は Xは Eのみの関数となっており、 Yを生成する式にはEは含まれていないことに注意してください。

このデータに対してYをXで回帰した回帰分析は以下のようになります。

f:id:takehiko-i-hayashi:20170918151915p:plain:w275

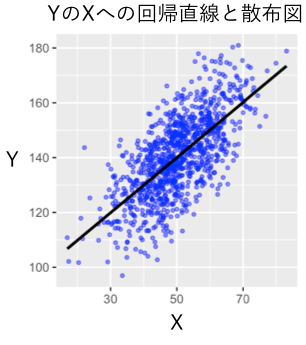
lm.res3 <- lm(Y3 ~ X3)
summary(lm.res3)
## 
## Call:
## lm(formula = Y3 ~ X3)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -31.356  -7.180   0.016   7.369  31.698 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 89.68687    1.73408   51.72   <2e-16 ***
## X3           1.00638    0.03383   29.75   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.71 on 998 degrees of freedom
## Multiple R-squared:   0.47,  Adjusted R-squared:  0.4695 
## F-statistic:   885 on 1 and 998 DF,  p-value: < 2.2e-16

Xの回帰係数（”Estimate”）の正解は予式1より「1」ですが、 n=1000とサンプルサイズも十分にあるので「1.00638」と高い精度で推定されています。つまり、 Xは内生変数ですが、今回のケースではバイアスは生じていません。

Xと「誤差」の相関をみてみましょう。


f:id:takehiko-i-hayashi:20170918152117p:plain:w275

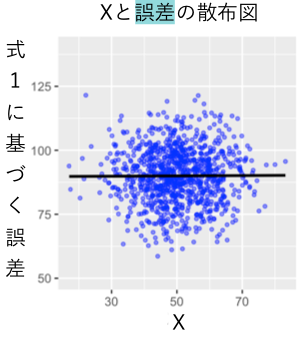
この場合には、 Xと「誤差」の間には相関はありません。（ここには示しませんが、最初の「内生性がないケース」と同様に、「残差」と平均値を補正した「誤差」の分布も重なります）

上記の例が示すように、ややこしいですが、内生性が生じる上では「 Xが内生変数であること（システムを表す方程式の内部で決定されていること）」自体が本質的な要因であるわけではありません*12。

より本質的なのは、「 X」と「誤差項」を決定する要因の中に共通ものがあるかどうかということになるわけです（下図／必要に応じて拡大などしていただければ幸いです）*13。

f:id:takehiko-i-hayashi:20170923073737p:plain

（やっと）まとめ

はい。今回もとても長くなってしまいました。いちおう所感をまとめておきます：

  • 内生性がないときは「誤差」と「残差」の分布は基本的に重なる（と期待できる）が*14、内生性があるときは「誤差」と「残差」は一般に重ならない*15
  • 回帰モデルが R^2値の観点から「良く適合している」ということと、そのモデルの説明変数の回帰係数がその「因果効果の良い推定値」かどうかは、本質的には別の問題である
  • 説明変数 Xが内生性をもつとき、「 Xの回帰係数」と「 Xへの介入効果の推定値」はズレる（バイアスが生じる）
  • 説明変数 Xが内生変数であっても、内生性をもつとは限らない。やれやれ。村（略）
  • 「誤差」をモデルに含まれていない諸要因の「関数」として敢えて決定論的な枠組みから眺めてみると、少し「説明変数と誤差の相関」というものが身近になるかも

-

  • けっきょくggplot2の使い方がやっぱり今ひとつ腑に落ちず自分の老いを感じた
  • ggplot2を使いこなすシャレオツな若者を見ると自分の老いを感じる
  • tidyverseを使いこなすシャレオツな若者を見ると自分の老いを感じる
  • Stanを使いこなすシャレオツな若者を見ると自分の老いを感じる
  • 最近までPythonの読みを「フィソン」だと思っていたことは絶対に秘密
  • あと環ROYのことも「かんろい」だと思ってた


はい。

本当は、これからさらに：

  • では、説明変数と残差に相関が出るのはどういうときなのか
  • 「説明変数と誤差の相関」と「共変量のバランシング」の関係

などについてものんびり眺めてみようと思っていたのですが、もう力尽きたので、ここに書くのはやめておきます。


というわけで今回の記事は終わりです。
今回も非常に長い記事をここまでお読みいただいた方、大変ありがとうございました！


＃わたくしごとですが、来る10月1日から、弊研究所内でのルーティン的異動により所内企画部に半年間の時限付き出向となるため、暫くのあいだブログやSNSの稼働率はさらに大幅に低下すると思いますがどもすみません。

＃RStudioで書いた今回の「Rコード＋解説メモ」をこちらに置いておきますので、お好きな方は適宜どうぞ！→ html, Rmd


【参考情報など】

横浜国立大の黒木学先生による、因果関係を関数的関係の連なりとして捉える「構造的因果モデル」の教科書がさいきん出ました。いわゆるPearlの体系とRubinの体系が理論的にはシームレスであることも解説されています*16。この内容が日本語で読めることの幸せたるや！激オススメです！

構造的因果モデルの基礎

構造的因果モデルの基礎


黒木先生の本はちょとまだ難しいかな・・・という方は、こちらをどうぞ。わたくしと黒木先生の共著によるバックドア基準の入門的解説原稿も収録されています。

岩波データサイエンス Vol.3

岩波データサイエンス Vol.3


「因果効果を調べたい目的変数の挙動はそもそもどの共変量のどのような関数でありうるか」を粘り強く考える習慣や技量*17を身につけると、内生性に対する考察だけではなく、交互作用の理解や一般化可能性に関する考察もより明晰にできるようになっていきます。因果推論における交互作用の解説については、以下のKRSK_phsさんの記事が激オススメです。とても大事なことが分かりやすく説明されています！
krsk-phs.hatenablog.com


おまけ：たまきろい*18。ことの次第。ことばの因果的連関。凄い。

環ROY / ことの次第

*1:個人的には、ここの「信頼されるものとはなりえない」という全称的-ゼロイチ的な記述は強すぎるように感じます。一致推定量からのズレも実務上は「程度問題」だったりするので（構造的因果モデル的に言うとバックドアパスにも太いのと細いのがあるっていう話）、感度分析でもしてもう少し粘り強く「どれくらい信頼できるか」を考える方向を尊重してほしいように思ったりするところです

*2:わたくしの中での村上春樹のイメージは『世界の終わりとハードボイルド・ワンダーランド』くらいで止まっておりますが申し訳ありません

*3:誤差そのものは「差」を表す表現ですが、個々のデータにおける「誤差」ではなくデータ全体に含まれる「差の総体」を議論の対象とする場合には、「誤差」は実質的に「バラツキ」を指すと考えられるため、ここでは「偶然により生じるバラツキ」という表現を用いています

*4:つまり、単なる等式ではなく、生成メカニズムの表現としての構造方程式である

*5:ここで式1をYの式ではなく y_{i}の式として記述しているのは、誤差項がなく完全に決定論的に定まっていることを強調することを意図しました。ここはどう書くかちょっと迷いました

*6:この相関行列の作成に関しては http://statmodeling.hatenablog.com/entry/scatter-plot-matrix のコードを参考にさせていただきました。多謝でございます

*7:式1の上ではYはDの関数でもあるのですが、データ上では明瞭には見えてないですね。Dの分散が小さいからかもしれません

*8:あるいは、回帰分析において両者の分布は「ぜひとも一致しておいてくれないと本当は色々と困るという事情により一致するのが当たり前だという期待が広く共有されているかもしれません」と記述した方がもしかしたら事態の正確な記述に近いのかもしれません

*9:構造的因果モデル的にいうとXとYの間のバックドアパスが閉じていないとき

*10:介入効果の推定の観点からは”過剰”という意味です。単なる予測モデルとしての観点からは特に問題はありません

*11:以前にも述べましたが、本稿では（モデルを構造方程式で表現したときに） X自体が他の変数の関数となっているとき、 Xを内生変数と呼びます

*12:というか内生変数の議論における「システム」の境界って誰が決めるんですかね？構造的因果モデルの観点から見ると、d分離によって議論すべき「システム」の境界はDAGの構造から理論的に定まりうるのだけれど

*13:構造的因果モデルの用語を用いてより正確に述べると「閉じていないバックドアパスがあるかどうか」

*14:「誤差」の定義にもよるかもしれない

*15:偶然に重なることはあるかもだけど

*16:潜在反応モデルの構造的因果モデルの枠組みによる定式化の解説など

*17:変数間の関数関係のグラフィカルな表現がDAGとなります

*18:今年のつくばロックフェスでライブを観ました。ものすごくかっこよかった！！！

確率概念について説明する（第3-2-2回）：「あらゆる奇跡はありふれる」問題

統計 リスク

こんにちは。林岳彦です。いくらあなたが槇原敬之の大ファンで、どんなときもどんなときも僕は僕らしくありたいと思っていても、浮気がばれたときに「もう恋なんてしないなんて〜 いわないよぜったい〜」と歌ったら殴られると思うからそれだけはやめた方がよいと思います。TPOを大切に。


さて。

前回は「到達可能性（のフレーミング）」という観点から、「可能性と確率のあいだ」について考えてみました。

今回は、「あらゆる奇跡はありふれる」という観点から、「可能性と確率のあいだ」について考えてみたいと思います。


（今回もとても長くなってしまいました。いつもながら本当にすみません。。。）

大久保のゴール：「あらゆる奇跡はありふれる」問題

では、今回のテーマである「あらゆる奇跡はありふれる」問題について見ていきましょう。

この問題は、現実の具体的なできごとの「ありえなさ」を真正面から計算していくととんでもなく低い数値になりがち、というものです。

具体的な例で考えてみましょう。

まずは、2014年の3月28日金曜日に等々力陸上競技場で行われた、Jリーグ2014年第5節の川崎フロンターレvs名古屋グランパスの試合におけるフロンターレの大久保嘉人による68分のゴールを採り上げてみます（わたくしフロンターレサポなので）*1。

こちらがそのゴールの動画となります：
2014年3月28日 川崎 VS 名古屋 68分大久保嘉人ゴール - YouTube

この最終的な大久保のゴールに至るまでは実に28本のパスが繋がっています。パスが繋がった選手を追っていくと：

田中→小林→森谷→中村→大久保→森谷→中村→田中→森谷→中村→森谷→中村→森谷→ジェシ→井川→谷口→レナト→谷口→大島→ジェシ→田中→ジェシ→大島→小林→中村→森谷→小林→中村→大久保→ゴール

となっています。

さて。では、このような「28本のパスが繋がってゴールに至る」という過程においてありうる可能世界の数を単純に計算してみましょう。

自分のチームのプレーヤーは11人ですから、最初のボールを持っているのは11人のうちの誰かになります。そして、誰かがボールを持っているときにそのパスの潜在的な受け手は10人です。つまり、1つのパスの受け手に関して10通りの可能世界があることになります。上記の最終的な大久保のゴールに至るまでには28本のパスが繋がっています。すなわちそのような10通りの可能世界の分岐（パス）が28回繰り返されていることになり、その可能世界の数は11✕(10の28乗)になります。

11✕10の28乗というと、11✕10000000000000000000000000000です。

上記の動画において私たちが見るものは、11✕10000000000000000000000000000通りの可能世界の中の一つが実現したものといえます。

嗚呼。 穣。 まさに奇跡的なゴール、というべきなのかもしれません。


さらに試合全体でのパス数について考えてみましょう。この試合全体でのフロンターレの成功したパス数は563回でした*2。この「563本のパスが成功する」という事態においてありうる可能世界の数は、同様に計算をすると「11✕(10の563乗)」になります*3。

つまり、この試合で等々力競技場の観衆が見たものは、成功したパスにおける組み合わせだけを考えても
11✕10000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000
0000000000000000000通り
の可能世界の中のうちの一つが実現したものといえるわけです。

全宇宙の素粒子の数が10の80乗ということらしいですので*4、「11✕(10の563乗)」というのはもはや、大沢誉志幸ならずとも途方に暮れてしまうような大きな数と言えるでしょう。

これはやはり奇跡的な試合、というべきなのかもしれません。


しかしながら、より本質的に考えてみましょう。

そもそも、「あらゆる奇跡はありふれる」 のがこの世界の性質なのかもしれません。

『あの日 あの時 あの場所で きみに会えなかったら』：奇跡、奇跡、また奇跡

「あらゆる奇跡はありふれる」のがこの世界の性質とは、どういうことでしょうか。

小田和正の『ラブストーリーは突然に』という1991年のヒット曲をヒントに考えてみたいと思います。この歌は『東京ラブストーリー』という、「また夢になるといけねえ」というサゲのセリフで有名なドラマの主題歌だったので覚えている方も多いのではないでしょうか。

この歌の有名なサビの部分のフレーズは：

あの日あの時あの場所で　きみに会えなかったら
僕等は　いつまでも　見知らぬ二人のまま

というものです。

自分の恋人と「あの日あの時あの場所で出逢えた」のは奇跡なんだ、と感じさせるステキな歌詞といえます。確かに、恋人との出会いというものは奇跡なのかもしれません。

しかし、太陽のHatsugen Komachi Angelとも言うべき本ブログのソフィストケイテッドな読者さま方におかれましては：

  • 「あの日あの時あの場所」とか言い出したら大体何のときでも当てはまるし
  • あの日あの時あの場所できみに会えなくても、別の日の別の時の別の場所で別の「きみ」に会えたんでしょうねえ
  • 数年後に「見知らぬ二人のままだったほうが良かった」ってなることもあるよね

と心の片隅で思ってしまうのかもしれません。


まあ実際に、多くの「奇跡」というものはそういうものかもしれません。

特定のケースについて事後的に取り上げれば「奇跡的な話」と思えても、全体的に眺めれば単に「ありふれた話」に過ぎないんじゃないの、いうことはよくあります。


以下では、数値的に分かりやすい例として、「誕生日のパラドックス」について見ていきます。

『今日も誰かの誕生日』：ありふれた奇跡に関する計算

キリンジに『今日も誰かの誕生日』という曲があります。これも本当にいい曲です。


ほとんど出オチのような話ですが、「ある任意の日が自分の誕生日である確率」は1/365と高くはありません*5。しかし、もっと全体的に眺めれば「今日も誰かの誕生日」なわけです。上の動画で堀込泰行が唄い上げるように、ハッピーバースデー・トゥー・エブリワン！なわけです。


では。「ある任意の日が自分の誕生日である確率」の話は単純すぎるので、次は「n人がいる部屋に同じ誕生日のペアがいる確率」について考えてみましょう。

これはいわゆる「誕生日のパラドックス」として知られている問題です（誕生日のパラドックス - Wikipedia）。

まずは手始めの前フリとして、少し単純なバージョンとして、「n人がいる部屋に自分と同じ誕生日の人がいる確率」を計算してみたいと思います。

まず、1人目の誕生日が自分と異なる確率は(364/365)です。その確率を1から引くと、1人目と誕生日が同じ確率「1-(364/365)」になります。さらに2人目の誕生日も自分と異なる確率は (364/365)X(364/365)となるなので、2人のうちのいずれかと誕生日が同じ確率は [1- (364/365)^2]になります。これをn人まで拡張していくと、「n人がいる部屋に自分と同じ誕生日の人がいる確率」の答えは：

1- (364/365)^n

になります。グラフに描くと：

f:id:takehiko-i-hayashi:20151023215114p:plain:w350

となります。この「n人がいる部屋に自分と同じ誕生日のペアがいる確率」が0.5を超えるのは、n=253のときになります*6。


では今度は、「n人がいる部屋に同じ誕生日のペアがいる確率」について考えていきましょう。

計算のやり方として、1から「n人がいる部屋で全員の誕生日が異なる確率」を引く方法で考えていきます。まず、1人目と2人目の誕生日が異なる確率は(364/365)になります。さらに3人目も異なる確率は(364/365)X(363/365)、4人目も異なる確率は(364/365)X(363/365)X(362/365)になります。これをn人まで拡張すると、その答えは (364!)/[(365^n)\times (365-n)! ]になります（Wikipediaでの説明はこちら）。これを1から引いたもの、すなわち：

1- (364!)/[(365^n)\times (365-n)!]

が「n人がいる部屋に同じ誕生日のペアがいる確率」になります。グラフに描くと：

f:id:takehiko-i-hayashi:20151023215140p:plain:w350

となります。

ここで、「n人がいる部屋に同じ誕生日のペアがいる確率」が0.5を超えるのは、n=23人のときになります。一方、「自分の誕生日と同じ人がいる確率」が0.5を超えるのはn=253人でした。「自分の誕生日と同じ」というのと「誰かの誕生日が同じ」では、起こりやすさがかなり異なることが分かるかと思います。


この「誕生日問題」が示すのは、事後的に特定の組み合わせのみを採り上げると「起こりにくそう」なことでも、そのような組み合わせが起こりうる元となる組み合わせの数の多さを考えれば、単に「ありふれうる」ということです。

このような事例は、実際の統計解析の現場においても「多重比較の罠」などの形で少なからず出会うものです。「多重比較の罠」について興味がある方は、ぜひ以下の過去記事もご参照いただければと思います：

『Happy Birthday, Mr. President』：意志と確率

もちろん、上記のような「組み合わせの数」の問題だけが、「起こりそうもないこと」がよく起こる原因というわけではありません。

たとえば、申し遅れましたが、本日（この記事の公開日）10月25日はわたくしの誕生日です。これはものすごい偶然・・・ということではもちろんありません。これは意図的に本記事の公開日をわたくしの誕生日にしたからです。

このように、人間の意志が絡むと「起こりそうにないこと」は、いともたやすく「起こりうる」ことに変化します。

ここで、誕生日ネタということで、マリリン・モンローがジョン・F・ケネディに捧げた『Happy Birthday, Mr. President』を聴いてみましょう。いろいろな意味でドキがムネムネする映像です：


マリリン・モンローがジョン・F・ケネディにお誕生日の歌を唄うなんて「あまりに奇跡的」なシーンのようにも思います。しかし、それは寧ろ、さまざまな人間の意志が絡んだ「あまりに必然的」なシーンであったのかもしれません。

ハッピーバースデー・ミスタープレジデント - Wikipedia


「人間の意志が絡むと、起こりそうにないこともたやすく起こる」ということを頭の中に留めておくことは、実務的にも重要なことです。

リスク評価の結果としては「リスクは非常に小さい」としていたことがらが、人間の意志／悪意の介在によりたやすく起きてしまうことがあります。

そんなときになって私たちは、必要だったのは実は「リスク評価」ではなく「セキュリティ評価」だった、と気づくことになるわけです。


そして、気づいたときにはもう取り返しがつかないことも多いのです。


野坂昭如が、唄うように。


『じこはおこるさ』：後知恵バイアス

ひとつひとつの事象に着目すれば起こる確率が低いものでも、それが起こりうる機会がものすごくたくさんあるのならば、それは「いつかはどこかでは起こる」のだと言えます。

例えば、この世界で1日に走っている車の数、電車の数を考えれば、「いつか・どこかで」交通事故が起きるのは必然的とも言えるでしょう。



しかし、「いつか・どこかで」事故は起きるというのは予測できても、「いつ・どこで」起きるのかを予測することは非常に難しいものです。そこには本当に非常に大きなギャップがあるのです。

そして実は、このギャップというのは、何かが実際に起きてしまった後では非常に見えにくくなるものです。人間というものは、何かが起きてしまったときは、後から「それは予想可能だった」と思いがちなのです（後知恵バイアス）。この「後知恵バイアス」は、しばしば社会の中でアンフェアな帰結を生むことがあります。


前節で、「人間の意図が絡むと、起こりそうにないこともたやすく起こる」と書きました。しかし、この逆の「起こりそうにないことが起きた時には、人間の意志（悪意、あるいは度し難い過失）が絡んでいる」というのは必ずしも正しくありません。

しかしながら、世間ではこの「起こりそうにないことが起きた時には、人間の意志（悪意、あるいは度し難い過失）が絡んでいるに違いない」という決め付けがしばしば起きてしまいます（例えば、福島県立大野病院産科医逮捕事件 - Wikipedia)。


「起こりそうにない事故が起きた時に、そのときの担当者を吊るし上げてサンドバックにする」という"解決"策は、残念ながら、日本においてはしばしば目にするものです。そして、担当者をサンドバックにするときには、上述の「後知恵バイアス」が大活躍します。

「起こりそうにないことが起きた時には、人間の意志（悪意、あるいは度し難い過失）が絡んでいる」という考え方が正しいケースもあるのだとは、思います。しかし、特に病気・感染症・天変地異などの自然現象が絡むケースでは、「なにかが起こりうる潜在的な機会は実はものすごくたくさんある」ことも多く、たまたまそこに居合わせた担当者がベストエフォートをしていたとしても防ぎきれないケースも少なくないのです。

そのような場合には、担当者個人を吊るしあげてサンドバックにすることは、本当の解決にはならないばかりか、より本質的な構造的／組織的レベルでの重大な問題が不問とされることにより、未来の犠牲者を増やすことにも繋がりかねません。

もちろんあらゆる事故が起きないのが一番ではありますが、人間の為すことに「完璧」はなく、自然の為すことはあくまで気まぐれで、私たちが暮らすこの世界ではいつだって可笑しいほどのダイスが転がされつづけているのです。

事故はいつかどこかで起きるものです。もし事故が起きたときには、その「起こりそうになかったのに起きてしまった」ことについて、冷静さとフェアネスを大切にしながら、丹念に腑分けしていく必要があるのだと思います。

「可能性」と「確率」のあいだ：極小の面積をもつ可能世界群をどう足し算するのか

・・・とここまで書いてきて、あまり「可能性と確率のあいだ」の話をしていないことに気づきました。以下では、これまでの話を踏まえつつ「可能性と確率のあいだ」について書いていきたいと思います。


結論から言うと、「可能性」として「起こりそうもないこと」を取り扱うのは、比較的に簡単かもしれません。しかし、それを「確率」として取り扱うのは必ずしも簡単ではありません。

確率というものを「（規格化された）可能世界の面積」と捉える見方を過去記事で説明してきましたが、「非常に起こりそうもないこと＝極小の面積を持つ可能世界」がものすごくたくさんある場合に、それらの面積を「どう足し合わせるうるのか」という問題は ーーー 少なくとも実務的には ーーー 非常にやっかいな問題となります。


特に、さまざまに異なる条件が積み重なって起こることがらについては、その非常に小さい"確率"の数値を決めること自体が難しくなります。さらに、どこまでの条件の重ねあわせの組み合わせまで考えるのかも難しい課題となります。

例えば、「これから100年以内にある特定の堤防Aが決壊する確率」というものを真正面から考えてみるとします。ここで、「決壊」という事象に影響を与えうる条件にはさまざまなものがあります。例えば、今後100年間で上流側のダムや堤防の管理がどうなっていくのか、人口や産業構造の変化に伴って流域の河川水の使用量がどうなっていくのか、あるいはその下支えとなる地方自治体の財政状況がどうなるのか、あるいは時空間的な降雨量が地球全体の気候変動に伴ってどう変化していくのか、などなどさまざまな「条件」があり、それらの条件の積み重ねの上での「可能性」を考える必要があります。

「これから100年以内にある特定の堤防Aが決壊する可能世界は少なくとも1つあります」というのは簡単です。しかし、その「これから100年以内にある特定の堤防Aが決壊する可能世界」が、どれだけの条件の組み合わせの数に基づく諸可能世界群のうちのどのくらいの面積を占めるのか（どのようにそれらの可能世界の面積群を足し合わせることができるのか）、そしてそもそもどこまでの条件の重ねあわせの組み合わせまで考えるべきなのか、というのは真正面から考えると途方もなく難しい問いになります。


「さまざまに異なる条件が積み重なることにより起きる」ことがらにおいて「そのような条件の積み重ねの場合の数がものすごく大きい」という場合には、「可能性」と「確率」の間に ーーー 少なくとも実務的には ーーー また一つの大きなギャップ（「可能性」を「確率」という概念の枠組みにはめ込むことが困難な状況）が広がっているわけです。

まとめ：この可能世界に／で祝杯を

はい。今回はかなり雑駁になってしまいましたが、最後に今回の内容をまとめてみます。

  • 事後的に特定の組み合わせのみを採り上げると「起こりにくそう」なことでも、そのような組み合わせが起こりうる元となる組み合わせの数の多さを考えれば、単に「ありふれうる」
  • 人間の意志が絡むと、起こりそうにないこともたやすく起こる
  • その逆の「起こりそうにないことが起きた時には、人間の意志（悪意、あるいは度し難い過失）が絡んでいる」は必ずしも正しくない
  • 後知恵バイアスで人を殴るのは止めよう
  • 「さまざまに異なる条件が積み重なることにより起きる」ことがらにおいて「そのような条件の積み重ねの場合の数がものすごく大きい」という場合には、「可能性」を「確率」という概念の枠組みにはめ込むのは難しい


さて。

今回の記事では、古今東西の名曲をお供に「あらゆる奇跡はありふれる問題」について見てきました。

そんな今回の記事の締めの曲は、ceroの『Orphans』です。


あらゆる奇跡はありふれるのだと知りつつも、この名曲のように、私たちの可能世界において 「この世界」が有る／「この世界」に在る ことの奇跡を、cerebrateしてみるのも悪くはないのかもしれません。



＃このシリーズの次回記事では、「そもそも確率は在るのか／唯<この世界>論」問題について書いていきたいと思います。

余談：オススメの参考文献

「偶然」の統計学 (ハヤカワ・ノンフィクション)

「偶然」の統計学 (ハヤカワ・ノンフィクション)

今回の記事で扱った「あらゆる奇跡はありふれる」問題についてもっと詳しく知りたい人は、ぜひこの本を読むと良いと思います。とても面白かったです。オススメっす。

多宇宙と輪廻転生―人間原理のパラドクス

多宇宙と輪廻転生―人間原理のパラドクス

「この宇宙が存在すること自体が確率的に奇跡だよね」という話を深掘りしたい人には、この本がオススメです。分析哲学的にゴリゴリとせまっていく本です。ただし「この宇宙が存在すること自体が確率的に奇跡だよね」という問題意識そのものを共有していない人が読んでも、たぶん全く何が何のことやらピンとこないかと思います。

安全という幻想: エイズ騒動から学ぶ

安全という幻想: エイズ騒動から学ぶ

後知恵バイアスで人を殴ることについて考えさせられます。個人的には、刑事裁判における行為の責任の捉え方において「counterfactualがどう構成されるべきなのか」ということについて考えさせられました*7。「科学と公共政策」「科学と法」「STS」などに関心のある人にはぜひ読んでみてほしい本です*8。


.

*1:試合記録はfootball labより

*2:パス数656✕パス成功率0.858

*3:まあ連続して成功しているわけではないので本当はちょっと違う計算式であるべきではありますが

*4:参照: https://ja.wikipedia.org/wiki/%E3%82%B0%E3%83%A9%E3%83%8F%E3%83%A0%E6%95%B0

*5:めんどいので、うるう年のこととか、またそれぞれの日に誰かが生まれる確率における偏りとか、そういうのはとりあえず無視させてください

*6:参照：http://kah.s35.xrea.com/gameprob/drop.htm

*7:もし他の人が当時の血液製剤の担当者だった場合に、もっと事態は悪化していたという可能性も十分ありうるのではないか --- 少なくとも私には、実際の一連の担当者たちよりもこの案件についてより適切に対応できる自信はない

*8:あと未だに安部英医師が極悪人の類だと思っている人がいたらぜひ読んでみたほうが良い

確率概念について説明する（第3-2-1回）：「可能性」と「確率」のあいだ／ 到達可能性の線引き問題

統計 リスク

やっと会えたね（本能寺で）。林岳彦です。さいきんルンバを買いました。ルンバが動いているのを眺めるときに、「実はどこかで山本昌がこのルンバをラジコンで操作している」のだと想像しながらその動きを眺めるととても贅沢な気分になれます。おすすめのライフハックです。


さて。

確率概念についての記事については前編だけ書いて、1年以上も間が空いてしまいました。もう間男と呼ばれても仕方ありません。たいへん申し訳ありません。


前回（前編）では、「可能世界論からコルモゴロフの定理までを繋げる」話をしました。

今回（後編）では、前回の内容を踏まえて：

「可能である」という概念と「確率」概念のあいだのギャップ

について書いていきたいと思います。

（今回も長い記事になっております。本当にすみません。。）


前編のおさらいと補足：「様相論理と確率測度」の記事の追加

あまりにも間が空いてしまったので、まずは以下の前回記事を軽くおさらいしてみます。

確率概念について説明する（第3-1回）：可能な世界の全体を1とする — コルモゴロフによる確率の定理（前編） - Take a Risk：林岳彦の研究メモ

前回のまとめは以下の通りでした：

  • 「可能である」ということは「（近傍の）可能世界全体の部分集合」の形で捉えることができる
  • 様相論理の理路から「確率空間」を捉えることがもし許容されるならば、以下のように「確率」を捉えることができる
  • ざっくり言うと：「Aの確率」とは、（近傍の）可能世界全体における「Aが真である可能世界の部分集合」の「大きさ」である
  • もうちょい細かく言うと：（近傍の）可能世界全体において、関数Pが以下の3つの要件を満たすとき、P(Aが真である近傍の可能世界の集合)は「Aの確率」である
    • 0 ≦ P(近傍の可能世界の部分集合）≦ 1
    • P（近傍の可能世界の全体）= 1
    • 「Aが真である近傍の可能世界の集合」と「Bが真である近傍の可能世界の集合」に重なりがないとき、P（Aが真である近傍の可能世界の集合 ∨ Bが真である近傍の可能世界の集合）= P(Aが真である近傍の可能世界の集合) + P(Bが真である近傍の可能世界の集合)

上記のまとめを読んでもさーせんしょうじきちんぷんかんぷんです、という方は適宜前回の記事および前々回の記事をお読みいただければと思います。


はい。

では今回の記事では、この「可能世界／様相論理から確率概念を捉える」アプローチに基づき、4つの論点を参照しながら「可能性と確率のあいだ」について見ていきたいと思います。

（厳格にアカデミックな内容というよりも、当面はリスク分析者による楽屋話のようなものになるかと思いますので、気楽に読んでいただければと思います）


＊以下マニア向けの補足＊
前回の記事を書いた後に、前回の記事と同様に「様相論理の理路から確率空間を捉える」というアプローチをしている記事を見つけたので以下に少し補足しておきます。

一つ目は、Stanford Encyclopedia of Philosophyの”Modal Probability Logics”の項になります。

”Modal probability logic”では、以下のように「様相論理 Modal Logic」と「確率 probability」を関連づけした論理が紹介されています*1：

Modal probability logic makes use of many probability spaces, each associated with a possible world or state.

もう一つは、『Artificial intelligence』という本の「確率概念」の導入の項にありました。この本はクリエイティブ・コモンズなので以下から該当部が読めます：

Artificial Intelligence - foundations of computational agents -- 6.1.1 Semantics of Probability

上記では、確率概念と可能世界についてのっけから：

First we define probability as a measure on sets of worlds, then define probabilities on propositions, then on variables

と導入しており、本ブログの前回記事とほぼ同じ考え方になっています。

上記2つのサイトを見る限り、「可能世界／様相論理から確率概念を捉える」のは、ある程度一般性のあるアプローチと言えそうです。


（１）到達可能性の線引き問題：どこまでが「”近傍"の可能世界」なのか？

ではまずは、「到達可能性」の線引き問題を考えてみたいと思います。


前回の記事でのまとめでは「確率」概念について以下のように説明しました：

ざっくり言うと：「Aの確率」とは、この世界の近傍の可能世界全体における「Aが真である可能世界の部分集合」の「大きさ」である

この「説明」はもっともらしくはあるのですが、現実の問題を考える上では困ってしまうところもあります。

それはとりもなおさず：

「（近傍の）可能世界全体」というけれど、「近傍」ってどこまで含めるの？

という問題です。


ここでいちど用語法のおさらいをしておきましょう。「この世界の近傍の可能世界」というのは、「この現実世界＠」から大きく隔たらないような（＝この現実世界＠から到達可能な）諸可能世界のことを意味しています。例えば、「ある朝に目を覚ましたときにあなたが巨大な虫になっている」ことが真である世界というのは、「この現実世界＠」とは異なる物理法則や生物的法則が支配している世界であると考えられるため、「この現実世界＠」の「近傍（＝到達可能な）の可能世界」とは言えないでしょう。

では、どこまでの可能世界を『「この現実世界＠」から大きく隔たらないような（＝到達可能な）諸可能世界』として含めれば良いのでしょうか？

ここで私たちは、この世界から諸可能世界への「到達可能性」に関する線引き問題に直面します*2。


先ずは単純な例として、コイン投げの結果に関する「可能世界」を考えてみましょう。

コイン投げの結果（落下後のコインの向き）は、普通に考えると”オモテ”か”ウラ"かということになります。ただし可能世界としては、「落下後のコイン向きが”ヨコ”（落下後にコインが立つ）」という可能世界も普通に想定することができます。

ここで、私たちは「コイン投げの結果が”ヨコ”である可能世界」を「この世界の近傍の（＝到達可能な）」可能世界として含めるべきでしょうか？


現実的問題としては、コイン投げのケースについて確率的に考える場合には、「”ヨコ”なんて考えてらんねーよ」ということになるかと思います。

これは、私たちが私たちの世界における今までの経験に基づき、コイン投げに際しての確率的考察においては『「コイン投げの結果が”ヨコ”の可能世界」を「この世界の近傍の」可能世界として含めない』という判断を暗黙裡に行っていることを意味しています。

ここで注目してほしいのは、この判断自体の是非ではなく、現実世界における対象を扱う上では「この世界の近傍の可能世界の全体（=全事象）」を定めるために我々自身による何らかの判断（=”近傍"のdefine）が必要であるということです*3。

そしてこの「近傍の（＝到達可能な）可能世界の全体」の範囲が定まらないかぎりは「確率」は定義できません。対照的に、「可能性」という概念は「この世界の”近傍"の可能世界の全体」が定まらなくても成り立ちます。（例：Aが真の可能世界が少なくとも一つ存在する＝Aの可能性がある）

ここに「可能性」という概念と「確率」という概念のあいだのギャップの一つがあるわけです。


この「どこまでを”近傍"に含めるのか問題」は、リスク分析の実務においてはしばしば現実的かつ本質的な問題になります。

例えば、「原子力発電所に重大事故を引き起こす外部的要因が生じる確率」を考える際に、「可能な外部的要因の事象」として何をどこまで考慮に含めるかという問題を考えてみましょう。

「大地震」「大津波」「大噴火」「旅客機の墜落」「ミサイル攻撃」「ドローンによる攻撃」「特殊部隊によるテロ攻撃」「隕石の落下」「超能力者の念力による攻撃」「宇宙人によるレーザー攻撃」等々、要因として生じる事象についてさまざまなレベルの「可能世界」を想定することができるかと思います。

これらの例において、「この世界の”近傍”の可能世界としてどこまでを考慮に入れるのか」というのは、絶対的な正解のないいわゆる「線引き問題」になります。


そして、実はリスク分析においてしばしば最も本質的*4な作業のひとつは、この「この世界の”近傍”の可能世界（＝全事象）としてどこまでを考慮に入れるのか」というフレーミングの部分になります。

このフレーミングさえ終わってしまえばリスク分析に残るのはあとは単なるテクニカルなパズル解きだけである（≒ 計算機が充分に発達すればデータサイエンティストの手元に残るのはフレーム問題だけである）・・・というのは多少言い過ぎにしても、リスク分析の最終的なメッセージ自体がフレーミングの仕方に大きく左右されうるケースもあり、この部分はとても重要なものになるわけです。

・・・抽象的な話だと分かりにくいかもしれないので、少し例を出して考えていきます。


分析の結論（意思決定結果）がフレーミングの仕方に極端に依存するようなケースとして、地球温暖化対策についての意思決定において「マキシミン則」を適用する場合を考えてみましょう。

まず、マキシミン則について説明しておきます。Weblio辞書から引用（link）します：

マキシミンルール
意思決定理論の用語。不確実な状況のもとで，予想される最悪の事態を避けることを合理的とする行動決定の基準。ロールズが正義の原理を導出する際に用いたことで知られる。

はい。一般的にいうと、マキシミン則とは「最悪のケース（minimum）における効用」を「最大化（maximize）する」という意思決定規則になります。くだけた言い方をすると、最悪の事態をできるだけ「まし」なものにするという基準で意思決定を行うルールのことです。


さて。では可能世界の枠組みを用いて考えていきます。

地球温暖化問題において「最悪のケース（最悪の可能世界）」とは何でしょうか。私が考えを巡らした限りでは、地球温暖化の帰結における「最悪の可能世界」は、「人類が滅亡した世界」になるのかなと思います*5。

ここで、マキシミン則を適用してみましょう。「人類が滅亡した世界」のケースは少なくとも人類にとっては効用の下限であると考えられる*6ので、「最悪のケース＝人類が滅亡した世界」を防ぐためのいかなる方策もマキシミン則に拠れば「最悪のケースにおける効用を改善（＝人類滅亡の回避」）」するという理由により正当化されることになります。つまり、マキシミン則によって考えれば、あらゆる地球温暖化対策はその効果がどんな微弱なものであっても正当化されることになるわけです。

ここでありうるツッコミとして、『そうはいっても「人類が滅亡した可能世界」に到達する”確率"なんて低いんじゃないの？』というものがあるかもしれません。

この辺りがポイントのひとつになります。

マキシミン則を採るかぎり、"確率"の大小は問題になりません。この世界の現在のありようが「人類が滅亡する可能世界の少なくとも一つに到達可能」であるかぎり、マキシミン則を採れば「人類が滅亡する」という極端なケースを判断基準とした意思決定の話に帰着することになります。

一方、もし温暖化による到達可能な最悪の可能世界を「シロクマが絶滅した世界」と規定した場合には、マキシミン則に基づき「温暖化なんて超巨額の資金を使って対策をするほどのものじゃないよね」ということになるかもしれません。


上記の事例が示しているのは、「マキシミン則による意思決定」は「可能世界の到達可能性の線引き（＝”近傍”のフレーミング）」の仕方に決定的に依存しがちということです。

一般的に、ある「Xという行為」についての意思決定において「マキシミン則を採用」し、なおかつ「可能世界の到達可能性をかなり広く採る」と、「Xという行為」に関する効用の下限として「人類の滅亡」のような極端なケースが含まれてくるため、「Xという行為」についての絶対的な評価に繋がりがちになります。

例えば、有名な「パスカルの賭け（wikipedia）」というものがありますが、これは「神を信じるという行為」に対して「可能世界の到達可能性をかなり広く採る（＝「地獄という可能世界」は到達可能であるとする）」ことにより「神を信じるという行為」の絶対的な評価へ至るロジックの一種として解釈できるかと思います。


（もう少し異なる方向からのツッコミとして、「地球温暖化対策を行なったことによりかえって「人類が滅亡した世界」へ至るような可能世界もあるんじゃないの？*7」とか「「人類が滅亡した世界」を可能世界に含むのは温暖化に限らないですよね？」とかいうものがありうるかとも思います。こういう観点を含めると、マキシミン則では決定不能なので何か他の原理を持ち込んで考えるしかないですよね、となってきます）


はい。上記の例では、リスク分析（に基づく意思決定）の文脈において、その結論がフレーミングの仕方に強く依存する場合があることを見てきました。（もしかして勘違いされている方もおられるかもしれませんが、「リスク分析という営み」そのものと、「どのような意思決定則を用いるか」は基本的には別個の問題ですのでご注意ください。例えば、シミュレーションによるリスク分析の結果を受けてマキシミン則を適用するというのも普通にありえる話です）

上記の例ではマキシミン則（効用の下限に基づく意思決定則）を考えているのでフレーミングに極端に依存しますが、例えば「平均効用」を用いてもフレーム内に極端な可能世界（効用が無限小であるとか）が含まれる場合には同じような状況が生まれます*8。一方、「効用の最頻値」を考えると状況は比較的ロバストになります。ここで、「どのような意思決定則を用いるべきか」は個別の文脈に応じて考えるべきであり、それ自体が大きな論点となるものです。


はい。


というわけで、本稿では「諸可能世界への到達可能性の線引き問題」という観点から『「可能性」と「確率」のあいだ』について見てきました。

このように、「可能性と確率のあいだ」についてどう考えるのかは、リスク分析においては実務的かつ本質的な問題として常に／既に横たわっているものなのです・・・とさらに書き続けていきたいところなのですが、もうずいぶん長くなってしまったのでこの続きは別エントリーとして書いていきたいと思います。


＊次回は、『「この世界の確率の低さ」問題：あらゆる奇跡はありふれる』という論点について書いていきます。


＊以下マニア向けの余談＊
“確率"というものが「客観的」なものか「主観的」なものかという論点はしばしば論争の種になります。私自身は「確率とは間主観的概念である」という立場であり、確率概念についての「客観的確率」という捉え方については特にかなり否定的です。その理由は、私がベイジアンであるからというよりも、私がリスク分析の実務に関わる人間であるから、という側面の方が強いです。端的に言って、公共政策に関わるリスク分析においては「確率」が「客観的確率」である、という認識は殆どの場合において優良誤認に過ぎないように感じています*9。上で書いたように、そもそも公共政策におけるナマの問題群を「確率という概念の型」にどう押し込むかというところからして間主観的なフレーミングに依存する部分が大きいのです。そのため、私はリスク分析者としてのある種の規範的な感覚として、「客観的確率」というものを是認する気にはどうしてもなれないのです。（そして、リスク分析は ---公共政策における専門知による分析一般と同様に--- 「間主観的なもの」であるからこそ、合意、あるいは合意された手続、に基づくことが重要となるわけです）


参考文献

ワードマップ現代形而上学: 分析哲学が問う、人・因果・存在の謎

ワードマップ現代形而上学: 分析哲学が問う、人・因果・存在の謎

可能世界論も含めた形而上学の入門として。わたくし的には2014年に読んだ本の中でいちばん面白かったです。こういう本がたくさん出ると門外漢としてはとても嬉しいです。

可能世界の哲学―「存在」と「自己」を考える (NHKブックス)

可能世界の哲学―「存在」と「自己」を考える (NHKブックス)

可能世界論の入門として。

*1:ただし、上記引用からも分かるとおり、"Modal probability logic"は「一つの可能世界に対して一つの確率空間」を対応させているようなので、本ブログ前回の記事とは階層がひとつズレている話になっているようです。

*2:確率論のコトバで言いかえると、『「全事象」って、どこまで含めるの？』という問いに対応します

*3:その判断が意識的になされたものか否かに関わらず

*4:であるにもかかわらず日常実務的には軽視されがち

*5:異論は認めます

*6:異論は認めます

*7:ジオエンジニアリングとか

*8:「パスカルの賭け」は寧ろこっちに近いと考えるべきなのかもだけど、まあどっちでもいいかとも思います

*9:ただし、筆者の観測範囲にバイアスが存在する可能性あり

夏の因果推論祭りのフォローアップをこんなに遅れて書くつもりじゃなかった

統計 リスク

こんにちは。フリッパーズ・ギターの性格が悪い方こと林岳彦です。

さて。

私も大人でありますので本業に追われることもままあります。そして追われているうちにすっかりご無沙汰してしまいました。はてはて。去る7/11に行われた因果推論祭りについてもブログにはまだ何も書いておりませんでした。申し訳ありませんでした。

まだ色々と余裕がないので、以下、雑感の書き散らしになりますがどうかご容赦を：

なにはともあれご講演をいただいた星野先生＆黒木先生に感謝しております

いや本当に感謝あるのみです。大変ありがとうございました。

そして聴講にお越しいただいた方々に感謝いたします

おかげさまで130人の教室がほぼ満員状態になるほどの方々にお越しいただけました。
大変ありがとうございました。

告知がネットやtwitterを中心に広まったこともあり、それぞれに面識も無くまた特に共通のバックグラウンドもない方々が集まり、普段の学会や勉強会とは何かしら異なる雰囲気でした。正直、登壇したときは、いつもより聴講者が「得体の知れない」気がして、近年になく緊張しました。（話をしているうちに和らぎましたが）

幾人か「中の人」にお会いできました

はてなブログ等でご活躍されている幾人かの「中の人」に直接ご挨拶することができました。
直接ご挨拶するのは照れくさいような面映いような、でも嬉しいものですね。
今後とも是非ともよろしくお願いいたします。

セミナーのレベル設定について

レベル設定は難しかったですね。聴講者のバックグラウンドも知識レベルも様々であり、レベル設定が高すぎて付いていけなかった方も、逆に低すぎて物足りなかった方もおられたかと思います。せっかく来ていただいたのに申し訳ない気持ちでいっぱいです。。（皆それぞれお忙しい中で貴重な時間を割いて来てくださっているわけで社交辞令ではなく本当に申し訳なく思っています）

「Pearl vs Rubin」という"アングル"について

私の告知文のせいで「Pearl vs Rubin」というアングルでの議論になりましたが、（人間的な部分でのエピソードの面白さはともかくとして）両者の理論のそもそものスコープの広がりを考えると、「Pearl vs Rubin」というのはあまり両理論の面白さのコアの部分を引き出すアングルではないのかもなあとも思いました（←今更）。

Rubinの潜在的結果変数の枠組みは、実解析において頻繁に直面する、欠測値等を含む「観測されなかったデータ」に対するアプローチとして非常にgeneralなリーチを持つという理論的なワクワク感があります。

一方、Pearlの枠組みは、これまた実解析において頻繁に直面する、（例えば）重回帰分析での変数選択において（AIC等とは全く理論的なレイヤーの異なる）理論的規範を示すというワクワク感があったりします。

こういう理論的な「ワクワク感」にもっとフォーカスできれば良かったかもしれません。

傾向スコア法についての雑感

傾向スコア法の理解や使用において「Pearlの体系の知識は必要ない」と言われると、なんというか、「重回帰分析において偏微分の知識は必要ない」というセリフを聞いたときのようなモヤモヤをかんじるんですよね。いや、確かに、偏微分の知識がなくても重回帰分析はできますし、もしかしたら実際に重回帰ユーザーの大半は偏微分を分かってないかもしれないですが、いや、でも、さ、というような。

個人的な学習体験として、最初に星野さんの本を読んだ時には、傾向スコアの変数選択の部分については本当に天下り的に理解することしかできなかったんですよね。その後、Pearlの体系を学んでから星野さんの本の変数選択の部分を再読したら、いきなり「もう読んだ端から理解できる」という状態になってたんですよ。「傾向スコアとはバックドアに蓋をする合成変数である」という理解*1があると、もう本当に書いてあることがスルスルと（書いてあることがもう自明に感じて読んでいてもどかしさを感じるほどに）理解できるんですよね。

Rubin系の傾向スコアの説明だと、変数選択の部分は殆ど本質的にはempiricalな「How」の説明に終始しているのですが、Pearlの体系は変数選択に際して確固たる理論に基づくnormativeな「Why」の体系を提供してくれているんですよね。やっぱりnormativeな「Why」の部分も理解できていたほうが、（特に非典型的な例に遭遇した場合などに）強いのではないかと思います*2。

傾向スコアの理解においてPearlの体系を学ぶことの効用の具体例としては、例えば、「強い無視可能性」の持つ本質的重要性を理解できることが挙げられるかと思います。どうしても、傾向スコアを最初に理解する際には、「傾向スコア←共変量」のモデリングの仕上がり具体の吟味に引きづられてしまうのですが（c統計量の値とか）、本来の「強い無視可能性」の意味を考えれば、実は「応答変数に効いているもの」を変数として選択することが重要なんですよね*3。この辺りは、グラフィカルモデル経由で傾向スコアの概念を理解したほうが分かりやすいように思います（参考：ハーバード白熱教室 これからの因果推論を考えよう）。

参考：吉田さん＠Robins派の記事

＊こちらに「因果推論祭り」を実際にご聴講いただいた方（吉田さん＠Robins派）の感想もありますので合わせてどうぞ：
因果推論祭り、Tokyo.R、機械学習ハッカソンなどの話 - きのう何書いた?

大変ありがとうございます！＞吉田さま

なにはともあれ

夏の因果推論祭りにお越しいただいた方、いただけなかった方も、大変ありがとうございました。

はてなブックマークの「学び」の欄が研究不正の話題で埋まっていたりする昨今にあり、純粋な学術的面白さを目当てに東大にお集まりいただいた方々に囲まれて幸せな時間を過ごせました。

今後とも何卒よろしくお願いいたします

参考文献

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

統計的因果推論 -モデル・推論・推測-

統計的因果推論 -モデル・推論・推測-

統計的因果推論―回帰分析の新しい枠組み (シリーズ・予測と発見の科学)

統計的因果推論―回帰分析の新しい枠組み (シリーズ・予測と発見の科学)

医学的介入の研究デザインと統計:ランダム化/非ランダム化研究から傾向スコア、操作変数法まで

医学的介入の研究デザインと統計:ランダム化/非ランダム化研究から傾向スコア、操作変数法まで

  • 作者: 木原雅子,木原正博
  • 出版社/メーカー: メディカルサイエンスインターナショナル
  • 発売日: 2013/10/31
  • メディア: 単行本（ソフトカバー）
  • この商品を含むブログを見る
＊例えば↑の本なんかだと傾向スコアの変数選択のところは本当にempiricalな「How」しか書いてないんだよなあ...

*1:因果推論祭りの中で、この理解が適切であることを黒木さんに直接確かめることができました

*2:「因果推論」に関して言えば、Rubinの体系は「How」、Pearlの体系は「Why」についての体系であると感じています。なので、ハウツー的手法としてはRubinの方が洗練されていますが、「なぜそのHowが成り立つのか」を深く理解したければPearlの体系を学ぶのが近道であるように思います

*3:この点は星野本でも強調されているのですが、Pearlの体系を理解する以前は、天下り的にしか理解できませんでした

識別/生成モデルの観点から見たRubin/Pearlの統計的因果推論（＊既に一定の予備知識のある方向け）

統計 リスク

こんにちは。林岳彦です。ついに夏の統計的因果推論祭りが今週の木曜（7/10）に迫ってきました！

ちゃんと予定どおり開催されますので、参加申し込みをされたみなさま、台風に負けずにご来場いただければ幸いでございます。

さてさて。


この祭りに備えてさいきん改めて統計的因果推論の辺りを復習しているのですが、今回は自分のためのメモとして「識別/生成モデルの観点から見たRubin/Pearlの統計的因果推論」について書いてみたいと思います。（ひじょうにマニアックな内容になります）


（今回の記事は「統計的因果推論」に対して既に一定の予備知識がある読者を想定して書いていきますので、多くの方々には意味不明なものになるかもしれませんが大変申し訳ありません）

前置き：今回の元ネタとなる2つの記事の紹介

そもそものことを言いますと、今回の記事は以下の2つの記事にかなり直接的にインスパイアされて書かれたものです。なので、以下の記事をご一読の上でこの記事を読んだほうが、本記事が「そもそもどういうことを考えて書かれたのか」が分かりやすいかと思われます*1 。

(1)の伊庭さんの論文は、ベイズ統計の流行について「識別モデルと生成モデル」という観点から論じたものです*2。

(2)の筒井さんの記事は、社会学における「”因果効果”の推定（措置効果モデル系）」と「媒介による説明（回帰分析系）」を巡る変遷について書かれたものです。

今回の記事では、(1)の論文の「識別モデルと生成モデル」という観点から、(2)の記事の「因果効果の推定 vs 媒介による説明」というテーマについて書いていきます。

まずは用語説明：生成モデル・識別モデルとは？

では、まずは「識別モデル（discriminative model）」と「生成モデル（generative model）」という用語について見ていきます。

「識別／生成モデル」という語に関しては、人によってやや用法に幅があるようですが、まず上記の伊庭（2006）における説明を引用してみます（尚、本論文中では"discriminative model”の訳語として「判別モデル」という語が使われています）：

すでに述べたように、生成モデル（generative model）の考え方では、データの生成過程を条件付き確率で表現して、すべての変数の同時分布を書き下し、あとは必要に応じてベイズの公式を使う、というのが基本的な方針である。これに対して、与えられた目的に必要な条件付き確率のみを抜きだしてモデル化する考え方がある。ここでは、これを判別モデル（discriminative model）と呼ぶことにする。


この2つはあくまでもモデル化の上での相対的な方針であって「これが生成モデルで、これは判別モデル」といった絶対的な判断基準があるわけではない。むしろ、生成的なモデル化（generative modeling）と判別的なモデル化（discriminative modeling）のように「方針」としてとらえたほうがよいかもしれない。また、統計的情報処理の目的は「判別」ばかりではないので、一般には「判別的なモデル化」というより「部分的なモデル化」ということになる。


対立点をまとめると

生成モデル
全体をモデル化して、目的に応じてそれを変形して利用する。変形のためにベイズの公式を積極的に利用。
判別モデル
必要のない部分はモデル化しない。ベイズの公式はなるべく使わない。

ということになる。これは「ベイズ」と「非ベイズ」の古典的対立のエッセンスを抜き出したものにも見えるが、二項対立ではなく多数のモデルを整理する軸として提示されている点にちがいがあるし、内容的にもより幅が広くなっている。

はい。ニュアンスも伝わる良い説明だと思います（あやかりたいものです）。（当該論文が入手可能な方は面白いのでぜひ全文をご一読ください！）

一応もういちど地の文でもまとめると：

基本的には（広義には）、「先ずデータの生成プロセスをモデリングする」のを志向するのが「生成的なモデル化」、「生成プロセスをすっとばして所与のデータから直接問題を解く」のを志向するのが「判別的（識別的）なモデル化」という言い方ができそうです。

また、実践的には、前者は「生成プロセスを条件付き確率の形で記述→記述さえできれば後は変形してベイズで（さくっとあるいはゴリゴリと）モデルパラメータの計算」という形で、後者は「所与のデータ→基底関数を噛ます→直接問題を解く（問題を解く能力を最大化するようにパラメータを学習させる）」という形で解かれることが多いようです。


どちらのアプローチが良いかというのはケースバイケースとしか言いようがないとは思いますが、（識別／分類そのものが目的である場合の）一般論としては、データ生成プロセスが適切にモデル化可能な場合には生成モデルの方が良いものの、それ以外のケースでは識別モデルの方が良い、と言えるかと思います。


また、一般論として、生成モデルの難点の一つは『生成過程からのモデル化ということを徹底すると、いわば「世界全体」を生成する」ことになってしまい、大変なことになる』（上記の伊庭 2006 から引用）という面も挙げられるかもしれません。この世界の生成プロセスーーー因果の継起ーーーにはアプリオリなキリはないからです。

後述するように、Rubinの体系もPearlの体系も着眼点は違えど「生成過程からのモデル化」に基づく体系として考えることができます。以下では、それらの体系の中で「世界全体を生成せずに済ませる」ための手法として、「傾向スコア」や「バックドア基準」というものを捉えてみたいと思います。

識別／生成モデルの枠組みから見たRubinの統計的因果推論と傾向スコア

はい。では、識別／生成モデルの枠組みからRubinの統計的因果推論の枠組みを眺めてみたいと思います。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

上記の星野さんの本を読む限りでは、Rubinの枠組みは基本的には「潜在的結果変数／欠測値に関する生成モデル的アプローチ」に基づく体系であるように思われます。このアプローチの中で、「欠測データ」の生成プロセスや「反事実的データ（潜在的結果変数）」の生成プロセスを「条件付き確率の形」で全て記述することさえできれば、原理的には後はベイズで計算することができます。

しかしながら、それらの生成プロセスは多くの場合に複雑and/or不明瞭であり、条件付き確率の形で書き切ることは困難です。また、複雑なモデルになると、原理的にはベイズで計算できるとはいってもその実行はなかなか大変になってきます。

そこで、問題の単純化への「抜け道」として良く用いられているのが「傾向スコア」になります。

はい。で、この「傾向スコア」のアプローチは事実上、「条件の”割付"に関する部分を識別的モデル*3で置き換える」ものとして捉えることができるかと思います。

実際に、「傾向スコア」の有用性／汎用性というのは、一般論として「識別モデル」が持つ有用性／汎用性とほぼ重なる部分が多く、共変量と割付に関連する部分の「生成モデル」がよく分からない場合においてもその辺りは全部すっとばしてロバストな推定をもたらしてくれたりするわけです。

（一方、実務上で少し困るところは「傾向スコア算出のための良い（実用に足る）”識別モデル"が得られるかどうかは実際にデータを喰わせて”学習"させてみないと分からない」ところかもしれません。「適切な生成モデルが構築できるか否か」という見通しの方は事前知識から割りと立ちやすい気もするのですが、「良い"識別モデル"が得られるか否か」というのは、実際にやってみないと事前には見通しが立たない面が大きいように思います。これはつまり、例えば、競争的研究資金の申請時などに、「これからデータを集めて、傾向スコアで分析やります！」とまるっと書いてしまうと多少リスキーな面があるということです）


識別／生成モデルの枠組みから見たPearlの統計的因果推論とバックドア基準

さて。次は、Pearlの統計的因果推論の枠組みを眺めてみたいと思います。

統計的因果推論 -モデル・推論・推測-

統計的因果推論 -モデル・推論・推測-

統計的因果推論―回帰分析の新しい枠組み (シリーズ・予測と発見の科学)

統計的因果推論―回帰分析の新しい枠組み (シリーズ・予測と発見の科学)

上記の本を読む限りでは、Pearlの統計的因果推論の体系が常用するところの非巡回有向グラフは正に「データ生成プロセスの図像化」みたいなところがありますので、Pearlの体系はモロに「生成モデル的」であると言えます。

で、「あまりに生成モデル的」であるPearlの体系において、それでも「世界全体を生成せずに済ませる」ことを可能にしているのが、「バックドア基準」であると言えるかもしれません。因果効果／措置効果の推定のためには「生成モデルのどの部分までを考慮に含めれば良いのか」という問いに対して、バックドア基準はその「生成モデルの”切り取り方"」を明晰に示すものになります。


とは言え、実際のケースにおいて「切り取り方が明晰に分かる」ためには既に一定程度以上にその生成モデル（非巡回有向グラフ）が明確になっている必要があり、そのような状況でない場合には、傾向スコア解析のような「識別的モデル」を利用した方が実務上は有効な場合が多くなります。

あるいは、Pearlの体系側から見ると、非巡回有向グラフの構造が一部不明瞭な場合に、「バックドアパスに蓋をするための合成変数を識別モデルにより作成してまとめて蓋をする」というアプローチが「傾向スコア」であるという捉え方もできるかもしれません。（＊この理解でおそらく正しいと考えていますが、木曜日に黒木さんに確認してみようと思います）

因果推論と識別／生成モデルの周りをぐるぐると巡る

さて。冒頭にご紹介した筒井さんの記事では以下のような記述があります：

因果推論を志向するアプローチと、媒介による説明を志向するアプローチは、この記事でも書きましたが、実は少なくとも回帰モデルにおいてはそれほど異なった分析を生み出すわけではありません。異なってくるのは、因果推論が回帰モデルから離れて、措置効果モデルによって純粋に介入の因果効果を追求するときからです。実験に範をとったこのモデルでは、純粋に原因（介入）と結果の関係を推定するがゆえに、回帰分析では可能であった媒介要因による説明のプロセスが抜け落ちます。観察データに適用される措置モデルでは、外生的な共変量でバランスを取った上で措置の効果を推定するという手続きがとられますので、措置はすでに媒介ではないわけです。逆に言えば、説明のプロセス（≒理論）をスキップできることが統計学の「強さ」の源でもあるわけです。


（...中略...）


因果が複合的に決定されていて、したがってSUTVA違反がむしろ社会の常態であることは、社会学者の感覚としてはある程度共有されているはずです。そうではないと、パネルデータ分析にあまり関心が向かず（ここ最近社会学者のあいだでパネル調査プロジェクトに参加していて、社会学者がいかに措置効果モデル的な因果推論に関心がないのかを痛感しました）、検定といえば個々の係数の効果の検定ではなくログリニアモデルやSEMなどの確証系分析を好み、措置効果モデルよりは複数の変数間の関係を捉えることに向いている回帰モデルを長く愛用してきたという、一見奇妙な計量社会学の傾向性を理解できません。

ここで、「措置効果モデル」というのは、本記事で述べてきたところの傾向スコア解析のような「生成モデルをすっとばす因果推論モデル」に対応するものです。また、「媒介要因による説明のプロセス」というのは正に「生成モデル的アプローチ」による解析に対応するものと考えられます。（この筒井さんの記事もとても面白いのでぜひ全文をご一読ください！）

上記のような社会学者の「因果推論と識別／生成モデル」をめぐる逡巡は、「因果推論とRubin／Pearlの体系」をめぐる逡巡とも相似形を成しているように思います。

識別モデル的な因果解析はクリアカットかつロバストな因果推論をもたらすので有効だし、Pearl的な非巡回有向グラフを用いた「生成モデルからの因果推論」もまた捨てがたし、というようなぐるぐると巡る気持ち、そんな、「同級生のみゆきと妹のみゆき」の間でぐるぐると巡るような気持ち、のまま本記事は終わりたいと思います。


そして来る木曜日は夏の統計的因果推論祭りがやってきます。

【参考文献等】

(1) グラフィカルモデル入門／川本一彦さん＠slideshare
(2) 社会学と因果推論 - 社会学者の研究メモ
(3) 伊庭幸人 (2006) ベイズ統計の流行の背後にあるもの. 電子情報通信学会技術研究報告. NC, ニューロコンピューティング 106(279), 61-66, 2006-10-04
(4) 久保さんの日記の6/19や
6/20 に収録のつぶやきが本記事を書くきっかけとなりました。多謝です。


.

*1:CiNiiが利用不可の方は大変申し訳ない

*2:そもそものそもそもの話を言えば、元々は久保さんの日記にある6/19や[ http://hosho.ees.hokudai.ac.jp/~kubo/log/2014/0611.html#10:title=6/20]における識別/生成モデルに関するつぶやきにインスパイアされてこの論文にたどり着きました

*3:一般的にはプロビット回帰やロジスティック回帰モデルが用いられる。ノンパラメトリックなカーネル回帰を用いる場合もあるらしい→『調査観察データの統計科学』p55, p62参照

【速報告知】渾身のガチ企画：『夏の統計的因果推論祭り』を開催します！（7月10日＠東大本郷）＊5/23登録締切りました＊

統計 リスク

（2014/5/23追記）＊参加希望者が予定人数に達したため登録を締切りました！＊
（2014/5/23追記）＊また、参加人数が予想を超えたため「14号教室」→「15号教室」に変わりました＊

こんにちは。林岳彦です。赤い彗星の測度は3倍です。

さて。

ここ数年にわたり半可通の分際で統計的因果推論について書き散らしてきたことの罪滅ぼしも兼ねて、以下のセミナーを開催いたします。

わたくしとしては渾身の100%ガチ企画でございます。2014年夏、「統計的因果推論」に興味がある全ての方々のご来場をお待ちしております！*1

第42回　リスク評価勉強会（FoRAM）
日時：7月10日（木）13:30～17:30 *2
場所：東京大学本郷キャンパス工学部1号館1階14号教室15号教室（MAP）


『統計的因果推論セミナー：相関から因果を取り出す1つの原理をめぐる2つの話』
（通称：『夏の統計的因果推論祭り』）


13:30-13:40　林岳彦（本セミナー企画者：国立環境研）
『前説：確率のレイヤーと因果のレイヤー』


13:40-15:10　星野崇宏さん（東京大学）
『Rubinの潜在的結果変数の枠組みによる統計的因果推論：傾向スコア、およびより発展的な話題（仮）』


15:20-16:50　黒木学さん（統計数理研究所）
『Pearlのグラフィカルモデルの枠組みによる統計的因果推論：バックドア基準、およびより発展的な話題（仮）』


16:50- 全体の質疑応答

  • 今回のセミナーはどなたでも聴講可能ですが、人数調整のため聴講には事前登録が必要です
  • 聴講希望の方は、事前登録のためのメールを事務局（foram-desk-ml@aist.go.jp）宛へお送りください（メールのタイトルは『夏の統計的因果推論祭り聴講希望』とし、本文にお名前とご所属をご記入ください）
  • 事前登録人数が予定数に達し次第、登録を締め切らせていただきます
  • 聴講者に必要とされるレベルとしては「少なくとも分散分析と重回帰分析は理解していること」を想定しています


ちなみにもちろん：

星野崇宏さんと言えば、以下の名著の著者であります：

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

そして黒木学さんと言えば、以下のPearl本の訳者でございます：

統計的因果推論 -モデル・推論・推測-

統計的因果推論 -モデル・推論・推測-

ガチでしょ？ ガチです。100%ガチの講師陣です。


今回のセミナーでは質疑応答の時間も長く取っておりますので、上記の本で分からなかった部分なども（もしあれば）、直接ご質問できる機会もあるかと思います（たぶん）。


繰り返しとなりますが、わたくしとしては渾身のガチ企画でございます。

ぜひ皆様のご来場をお待ちしております！


追伸：本セミナーの講師をご快諾いただいた星野崇宏さん、黒木学さんに改めて心より感謝申し上げます。本当にありがとうございます。

*1:とはいえ、会場サイズによる人数制限がありますので、「我こそは!!」という方はお早めの事前登録をお願いいたします

*2:時間・内容は多少変更の可能性があります

確率概念について説明する（第3-1回）：可能な世界の全体を1とする — コルモゴロフによる確率の定理（前編）

統計 リスク 統計 リスク

こんにちは。林岳彦です。先日、小学生の息子とセブンイレブンに行きました。そこでふと、「あの外壁、あれ本物のレンガじゃなくてただの印刷だから」と息子に教えたところ、それが彼にとっては思いもよらぬことだったようで、実はすべすべとしている外壁に触っては「すっかり騙されてた！（ガーン）」と衝撃を受けていました。小さな子どもをお持ちのみなさま、この世の隠蔽された真実（＝セブンイレブンの外壁は印刷）を彼ら／彼女らに教えてみると面白い反応が期待できるかもですよ！


さて。


今回は、前回の記事の続きとして、確率という概念の「規格」について説明していきたいと思います。

（今回はとても長い上に内容がハードかもしれません。いつもながらすみません。。）

前回の軽いまとめ

前回の記事では：

少なくとも、「確率」とは「可能性を数値で表したもの」である

というボンヤリとした出発点から：

「可能である」ということは、「この現実世界＠」の近傍の可能世界の集合の枠組みにより表すことができる

というところにまで到達することができました。 （まだ前回の記事を読んでいない方は、そちらをあらかじめお読みください）

今回は、その各々の「可能である」ことの程度を「数値で表す」ためのアプローチ（＝確率測度）について説明していきます。


（尚、本シリーズの説明では、数学的／論理学的な厳密性よりも、『可能である』というcrudeな概念が、数学的概念としての『確率』というformalな概念とどういう関係性にあるのか、という部分を示すことをその野心としているため、数学的／論理学的な説明としては不十分な部分が散見されるかもしれません*1。申し訳ありませんが、確率測度や様相論理についてのきちんとした説明をお求めの方は、別途参考文献の方をご参照いただければと思います*2）

可能世界全体の部分集合を考える

前回の記事では、「Aは不可能である／可能である／必然である」という表現を一般的な形でまとめると：

  • 「Aは不可能である」＝「全ての（近傍の）可能世界においてAは偽である」
  • 「Aは可能である」＝「Aが真である（近傍の）可能世界が少なくとも1つある」
  • 「Aは必然である」＝「全ての（近傍の）可能世界においてAは真である」

と表せることを見てきました。 （ここでの「近傍」というのは「この現実世界＠」から見た場合のものになります）

これはつまり、「可能である」ということを「（近傍の）可能世界全体の部分集合」の形で捉えることができる、ということです。

図で表すと：

f:id:takehiko-i-hayashi:20140410163017p:plain:w400

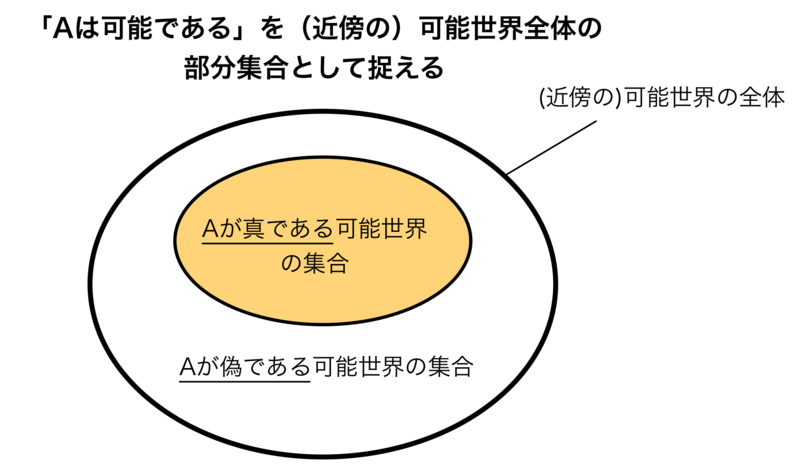
のようになります。大きな円は「（近傍の）可能世界の全体」を表し、オレンジの部分は「Aが真である可能世界の集合」、白の部分は「Aが偽である可能世界の集合」を表しています。

ここで、「Aが真である可能性」を数値で表したい場合には、この「オレンジの部分に対応する部分集合」に対して、何らかの数値を対応させていくことができれば良さそうです。以下では、そのようなアプローチを探っていきます。

（ここで、より本来的には、そもそも「（近傍の）可能世界の全体」自体が、「（荒唐無稽なものも含めた）可能世界の全体」の部分集合であることも視野に入れて考える必要があります。しかし、今回の記事では、「”Aの可能性"に数値を対応させる」という文脈において「荒唐無稽な可能世界」を含めて考えることに余り積極的な意味はない／そもそも「荒唐無稽な可能世界におけるAの真偽」について数値を対応させることやその数値について「足し算ができる」という性質を期待することが妥当ではないかもしれない、という理由により、「（近傍の）可能世界の全体」のみを念頭に考えを進めていきます）

（ちなみに、今回の記事において筆者の頭の中では、確率空間（Ω, F, P）について、「（荒唐無稽なものも含めた）可能世界の全体」が「Ω」、「（近傍の）可能世界の全体」が「F」に対応するというイメージになっています）

確率測度：（近傍の）可能世界全体の部分集合に数値を対応させる

では、（近傍の）可能世界の部分集合に数値を対応させることを考えていきましょう。具体例として、「A = 今から私が百円硬貨を投げたときにオモテが出る」という事象について考えていきます。

まず、今から私（筆者）が百円硬貨を投げると、その硬貨が投げられたときの物理的な軌跡（その空間上の位置や速度や回転の度合いetc..）には無数の場合がありうるでしょう。それらの「無数の場合」を、「投げられた百円硬貨の物理的な軌跡において異なる無数の（近傍の）可能世界」として捉えます。

それらの無数の可能世界に対して、百円硬貨が着地したときにオモテ面が出たかどうかに基づき集合を作成すると、結局のところ、「オモテが出る可能世界（Aが真である可能世界）」と「オモテが出ない可能世界（Aが偽である可能世界）」の２つの可能世界の集合に分けることができるでしょう。図で表すと：

f:id:takehiko-i-hayashi:20140410163114p:plain:w400

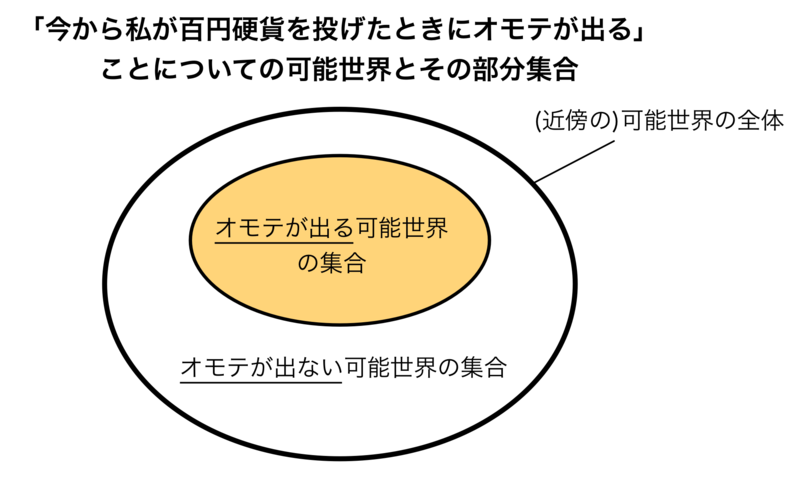
となります。大きな円は「（近傍の）可能世界の全体」を表し、オレンジの部分は「オモテが出る可能世界（Aが真である可能世界）の集合」、白の部分は「オモテが出ない可能世界（Aが偽である可能世界）の集合」を表しています。


ここで、『「オモテが出る可能世界（Aが真である可能世界）の集合」に数値を対応させる』のに先立って、その数値の大きさについてのとりうる範囲を定めておきましょう。

単純に考えて、その数値の潜在的な上限は「（近傍の）可能世界の全体における全ての可能世界がオモテが出る可能世界である」ケースに対応し、一方、数字の潜在的な下限は「（近傍の）可能世界の全体における全ての可能世界がオモテが出ない可能世界である」ケースに対応すると考えるのが自然でしょう。ここで、具体的には数値の下限を”0"、数値の上限を"1"とします。図で表すと：

f:id:takehiko-i-hayashi:20140410163140p:plain:w400

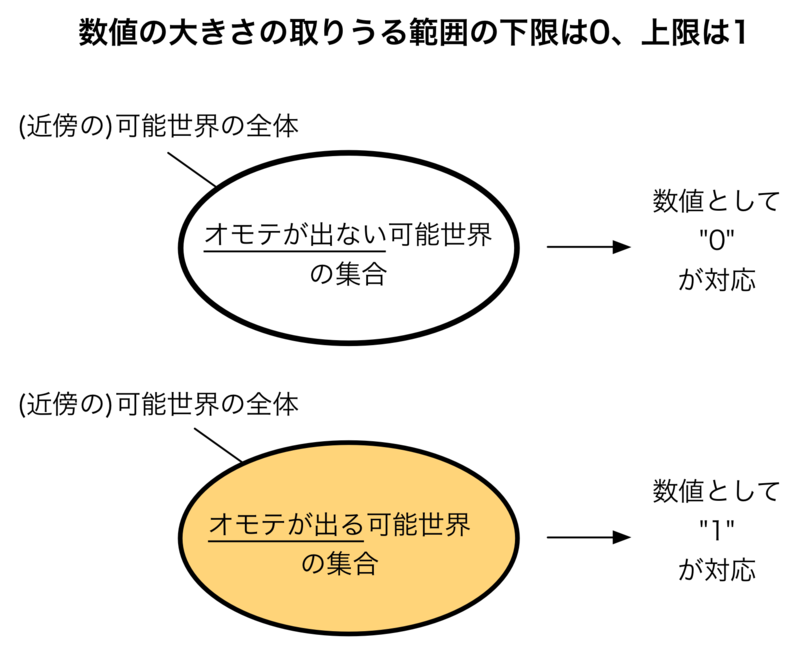
というイメージです。このとき、両者の中間のケースとなる「（近傍の）可能世界の全体における一部の可能世界がオモテが出る可能世界である」という場合には、0から1の間の数値が対応すると考えるのがしっくりくるかと思います。

f:id:takehiko-i-hayashi:20140410163210p:plain:w400

はい。

さて、では『「オモテが出る可能世界（Aが真である可能世界）の集合」に数値（実数）を対応させる』というアプローチ自体を図で描いてみたいと思います。いささか抽象的になりますが：

f:id:takehiko-i-hayashi:20140410163241p:plain:w480

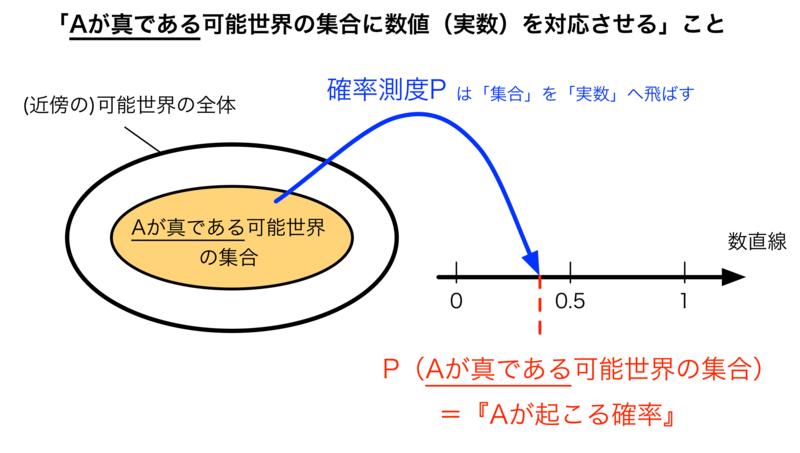
のように描けるかと思います。このとき、この上図における「P」 は「部分集合に対して実数を対応させる関数」であり、「確率測度」と呼ばれるものになります。そして、その関数により与えられた値である「P(Aが真である可能世界の集合）」が「Aの確率」となります。


抽象的すぎて分かりにくいかもしれないので、具体例で考えてみましょう。例えば、「今から私が百円硬貨を投げたときにオモテが出る確率が0.5である」というのは、上記の枠組みにおいて、「P(今から私が百円硬貨を投げたときにオモテが出る可能世界の集合) = 0.5」に対応します。「P」 は「今から私が百円硬貨を投げたときにオモテが出る可能世界の集合に対して、0.5という実数を対応させる関数」となっています。（ここで”0.5”という数字が対応することの正当性については、確率の「規格」ではなく「内実」の方に関わる問題になります*3）

f:id:takehiko-i-hayashi:20140410163306p:plain:w480

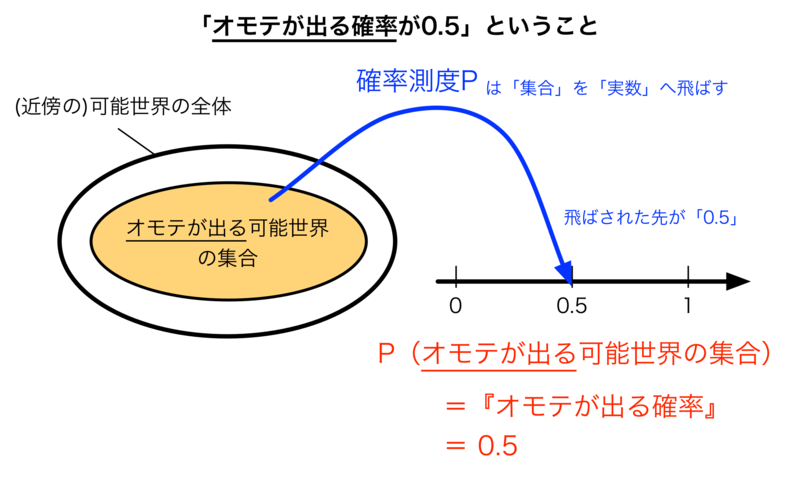
上記のように、ある「部分集合に対して実数を対応させる関数」によって「確率」を定式化するのが測度論的確率論の基本的な考え方になります。


測度論的確率論では通常、上記の「部分集合」が含まれる「全体」に関しては、今回のような「可能世界の集合」という言い方はせずに、「諸事象の全体」としての抽象的な「確率空間」というものを最初に想定した説明がなされます。逆に言うと、その「確率空間」と「様相論理／可能世界論」のパラレリズムを明示的に意識しながら確率測度について説明する、というのが今回の記事の骨子となっています（参考→： at_akadaさんによる「確率空間」と「可能世界論」の読み替えメモの記事）。


ここで「測度」というのは「大きさ」というものに関する一般的な概念であり、例えば、数学的には「面積」というものは、2つ組の実数からなるユークリッド空間全体における「部分集合」に対して実数を対応させる関数（測度）により定式化されています。この「面積」と同様に、「確率」は数学的には「確率空間／可能世界全体」における「部分集合」に対して実数を対応させる関数（確率測度P）によって定式化されているわけです。

で。

もちろん、その「部分集合に対して実数を対応させる関数（確率測度P）」というものは「関数だったらなんでもよい」というわけではありません。「確率測度」と呼ばれるためにには、以下の「コルモゴロフによる確率の公理」の要件を満たしている必要があります。

というわけで、「コルモゴロフによる確率の公理」について以下で見ていきましょう。

（とは言っても、実は、これまでの「確率」の説明においてあらかじめ確率の公理の要件を満たすように話を進めてきているので、実質的にはおさらいの形になります）

コルモゴロフによる確率の公理

Wikipedia先生によるとコルモゴロフによる確率の公理は次の通りです：

確率測度の定義は、コルモゴロフによる次のような確率の公理の形にまとめることが出来る。

  • 第一公理: 全ての事象の起きる確率は 0 以上 1 以下である; 0 ≤ P(E) ≤ 1 for all E ∈ E 。
  • 第二公理: 全事象 S の起きる確率は 1 である; P(S) = 1 。
  • 第三公理: 可算個の排反事象に関する和の法則が成り立つ; {Ek}k∈N が、どの二つも互いに共通部分を持たないような E の元の可算列ならば

　　　　　f:id:takehiko-i-hayashi:20140409221906p:plain

この第一公理は、任意の事象E（= 任意の（近傍の）可能世界の部分集合E）に関してその確率P(E)は「0以上1以下」になるというものです*4。具体的に言うと、P(今から私が百円硬貨を投げたときにオモテが出る)が「0以上1以下」の範囲の値である、ということになります。本記事の説明においても、P（近傍の可能世界の部分集合）は「0以上1以下」範囲の値をとるとしているので、この公理が満たされています。

次の第二公理は、「全事象の確率は1である」というものです。本記事の説明においても、P（近傍の可能世界の全体）= 1としているので、この定理が満たされています。

最後の第三公理は、各事象（＝近傍の可能世界における各部分集合）に重なりがない（排反な）場合に、確率の「足し算」が成り立つということです。これは例えば、事象A（＝Aが真である可能世界の集合）と事象B（＝Bが真である可能世界の集合）に重なりがない場合に、P(A ∨ B) = P(A) + P(B)が成り立つというものです。P(A)とP(B)がそれぞれ事象Aと事象Bの確率空間（＝可能世界の全体）内における"面積"のようなものに対応するものと考えれば、この足し算が成り立つのは自然なものであると考えられます。

はい。

というわけで、今回の記事では：

「可能である」ということは、「この現実世界＠」の近傍の可能世界の集合の枠組みにより表すことができる

というところから出発し、コルモゴロフによる確率の公理までたどり着くことができました。

（もし説明が煩雑すぎて途中で遭難してしまっていたらすみません。。）

今回のまとめ

はい。

では、今回の内容をまとめます：

  • 「可能である」ということは「（近傍の）可能世界全体の部分集合」の形で捉えることができる
  • 様相論理の理路から「確率空間」を捉えることがもし許容されるならば*5、以下のように「確率」を捉えることができる
  • ざっくり言うと：「Aの確率」とは、（近傍の）可能世界全体における「Aが真である可能世界の部分集合」の「大きさ」である
  • もうちょい細かく言うと：（近傍の）可能世界全体において、関数Pが以下の3つの要件を満たすとき、P(Aが真である近傍の可能世界の集合)は「Aの確率」である
    • 0 ≦ P(近傍の可能世界の部分集合）≦ 1
    • P（近傍の可能世界の全体）= 1
    • 「Aが真である近傍の可能世界の集合」と「Bが真である近傍の可能世界の集合」に重なりがないとき、P（Aが真である近傍の可能世界の集合 ∨ Bが真である近傍の可能世界の集合）= P(Aが真である近傍の可能世界の集合) + P(Bが真である近傍の可能世界の集合)

はい。こんなかんじでしょうか。

で。

あのですね。

もしかすると、数学のセカイから「確率」を眺めている方々にとっては、今回の記事は「野暮の極み」に映っているのかもと想像しています。

なぜかというと、そもそもこういう可能世界論みたいな「哲学的なんちゃらかんちゃら」との関わりあいをキレイに避けられるのが「確率空間」とか「確率測度」みたいなものを援用して考えることの利点でもあるからです。

まあそれは確かにそうなのです。ですが、実務的な観点から言いますと、可能世界論から「確率」を捉えることには：

「可能である」という概念と「確率」概念のあいだのギャップ

を明晰に理解できるようになるという、大きな利点もあるのです。

この「ギャップ」を理解しておくことは、現実のナマナマしい案件を確率論的モデリングの世界に落とし込む際にとても重要になります。


今回の記事の後編として、次回の記事ではその『「可能である」という概念と「確率」概念のあいだのギャップ』について書いていきたいと思います。

<参考文献>

プログラミングのための確率統計

プログラミングのための確率統計

のっけから測度論的なアイデア*6からの確率概念の説明がされています（そして、その説明の仕方がほとんど可能世界論的です）。書きぶりがとても面白くて親切で、個人的には確率統計の教科書としてとても大好きな本です。プログラミングはほとんど関係ないのに『プログラミングのための』という題名になっていることで読者が限定されてしまっている気がするのだけが残念です。本当に良い本だと思います。みんなこの本を読めばいいのにと思います。

応用のための 確率論入門

応用のための 確率論入門

ガチの測度論から導入される確率論の教科書です。こちらの本の語り口も大好きです（私は数学力不足のためこの本の前半部しか理解はできていませんが）。とはいえ、こういうガチの測度論から入る本に「入門」というタイトルを付けるのは読者のミスマッチの原因になるのでやめた方が良いなあとは思います*7。いわゆる初学者向けの入門書の類ではありません！

<参考サイト>

雑記2008年3月26日(水) - うつし世はゆめ / 夜のゆめもゆめ
at-akadaさんによる可能世界論と確率空間の読み替えについてのメモです。参考にさせていただきました。多謝です。



.

*1:できるだけちゃんとした説明となるように頑張りましたが、正直限界も感じています

*2:尚、本シリーズの内容については、論理学／分析哲学畑の共同研究者と共に細部を詰めた後に、総説論文等の形で発表することを予定しています

*3:確率の「内実」に関わる、主観確率や頻度的確率等々の考え方については次々回以降に説明していきます

*4:ただしEは完全加法性を満たすとする

*5:そんなん認めないやい！という見解も当然ありだとは思います

*6:測度論そのものが解説されているわけではないですが

*7:勘違いして買った人がAmazonに酷評レビューを載せてるのを見るのは全方位的に悲しい