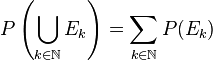確率概念について説明する(第3-1回):可能な世界の全体を1とする — コルモゴロフによる確率の定理(前編)
こんにちは。林岳彦です。先日、小学生の息子とセブンイレブンに行きました。そこでふと、「あの外壁、あれ本物のレンガじゃなくてただの印刷だから」と息子に教えたところ、それが彼にとっては思いもよらぬことだったようで、実はすべすべとしている外壁に触っては「すっかり騙されてた!(ガーン)」と衝撃を受けていました。小さな子どもをお持ちのみなさま、この世の隠蔽された真実(=セブンイレブンの外壁は印刷)を彼ら/彼女らに教えてみると面白い反応が期待できるかもですよ!
さて。
今回は、前回の記事の続きとして、確率という概念の「規格」について説明していきたいと思います。
(今回はとても長い上に内容がハードかもしれません。いつもながらすみません。。)
前回の軽いまとめ
前回の記事では:
少なくとも、「確率」とは「可能性を数値で表したもの」である
というボンヤリとした出発点から:
「可能である」ということは、「この現実世界@」の近傍の可能世界の集合の枠組みにより表すことができる
というところにまで到達することができました。 (まだ前回の記事を読んでいない方は、そちらをあらかじめお読みください)
今回は、その各々の「可能である」ことの程度を「数値で表す」ためのアプローチ(=確率測度)について説明していきます。
(尚、本シリーズの説明では、数学的/論理学的な厳密性よりも、『可能である』というcrudeな概念が、数学的概念としての『確率』というformalな概念とどういう関係性にあるのか、という部分を示すことをその野心としているため、数学的/論理学的な説明としては不十分な部分が散見されるかもしれません*1。申し訳ありませんが、確率測度や様相論理についてのきちんとした説明をお求めの方は、別途参考文献の方をご参照いただければと思います*2)
可能世界全体の部分集合を考える
前回の記事では、「Aは不可能である/可能である/必然である」という表現を一般的な形でまとめると:
- 「Aは不可能である」=「全ての(近傍の)可能世界においてAは偽である」
- 「Aは可能である」=「Aが真である(近傍の)可能世界が少なくとも1つある」
- 「Aは必然である」=「全ての(近傍の)可能世界においてAは真である」
と表せることを見てきました。 (ここでの「近傍」というのは「この現実世界@」から見た場合のものになります)
これはつまり、「可能である」ということを「(近傍の)可能世界全体の部分集合」の形で捉えることができる、ということです。
図で表すと:
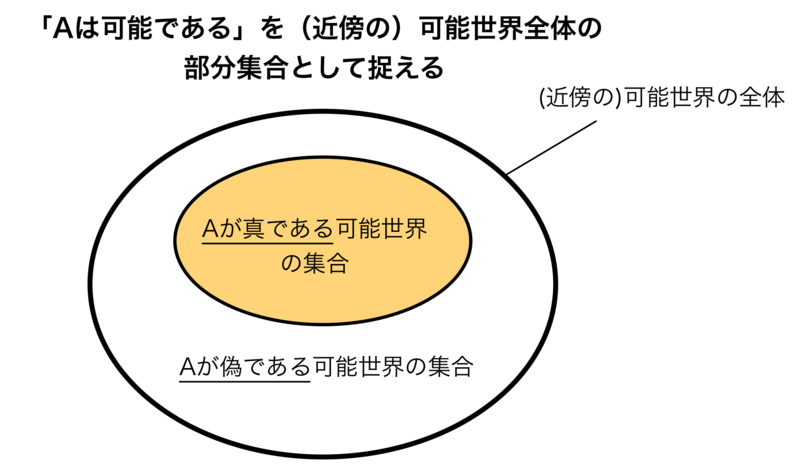
のようになります。大きな円は「(近傍の)可能世界の全体」を表し、オレンジの部分は「Aが真である可能世界の集合」、白の部分は「Aが偽である可能世界の集合」を表しています。
ここで、「Aが真である可能性」を数値で表したい場合には、この「オレンジの部分に対応する部分集合」に対して、何らかの数値を対応させていくことができれば良さそうです。以下では、そのようなアプローチを探っていきます。
(ここで、より本来的には、そもそも「(近傍の)可能世界の全体」自体が、「(荒唐無稽なものも含めた)可能世界の全体」の部分集合であることも視野に入れて考える必要があります。しかし、今回の記事では、「”Aの可能性"に数値を対応させる」という文脈において「荒唐無稽な可能世界」を含めて考えることに余り積極的な意味はない/そもそも「荒唐無稽な可能世界におけるAの真偽」について数値を対応させることやその数値について「足し算ができる」という性質を期待することが妥当ではないかもしれない、という理由により、「(近傍の)可能世界の全体」のみを念頭に考えを進めていきます)
(ちなみに、今回の記事において筆者の頭の中では、確率空間(Ω, F, P)について、「(荒唐無稽なものも含めた)可能世界の全体」が「Ω」、「(近傍の)可能世界の全体」が「F」に対応するというイメージになっています)
確率測度:(近傍の)可能世界全体の部分集合に数値を対応させる
では、(近傍の)可能世界の部分集合に数値を対応させることを考えていきましょう。具体例として、「A = 今から私が百円硬貨を投げたときにオモテが出る」という事象について考えていきます。
まず、今から私(筆者)が百円硬貨を投げると、その硬貨が投げられたときの物理的な軌跡(その空間上の位置や速度や回転の度合いetc..)には無数の場合がありうるでしょう。それらの「無数の場合」を、「投げられた百円硬貨の物理的な軌跡において異なる無数の(近傍の)可能世界」として捉えます。
それらの無数の可能世界に対して、百円硬貨が着地したときにオモテ面が出たかどうかに基づき集合を作成すると、結局のところ、「オモテが出る可能世界(Aが真である可能世界)」と「オモテが出ない可能世界(Aが偽である可能世界)」の2つの可能世界の集合に分けることができるでしょう。図で表すと:
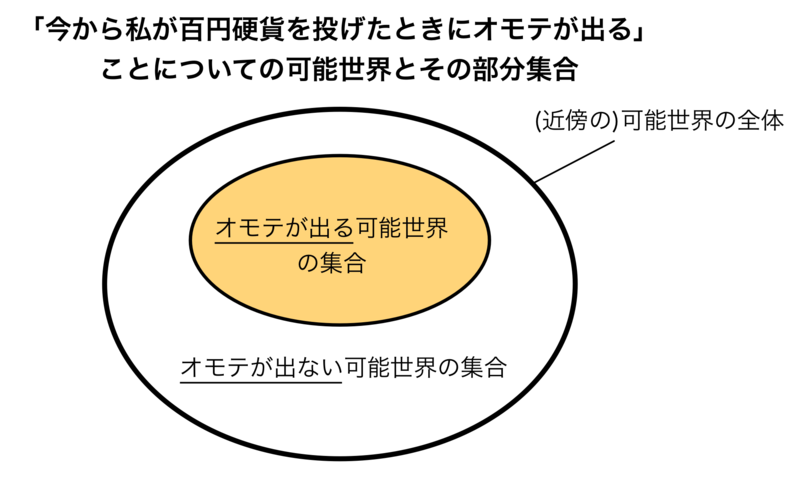
となります。大きな円は「(近傍の)可能世界の全体」を表し、オレンジの部分は「オモテが出る可能世界(Aが真である可能世界)の集合」、白の部分は「オモテが出ない可能世界(Aが偽である可能世界)の集合」を表しています。
ここで、『「オモテが出る可能世界(Aが真である可能世界)の集合」に数値を対応させる』のに先立って、その数値の大きさについてのとりうる範囲を定めておきましょう。
単純に考えて、その数値の潜在的な上限は「(近傍の)可能世界の全体における全ての可能世界がオモテが出る可能世界である」ケースに対応し、一方、数字の潜在的な下限は「(近傍の)可能世界の全体における全ての可能世界がオモテが出ない可能世界である」ケースに対応すると考えるのが自然でしょう。ここで、具体的には数値の下限を”0"、数値の上限を"1"とします。図で表すと:
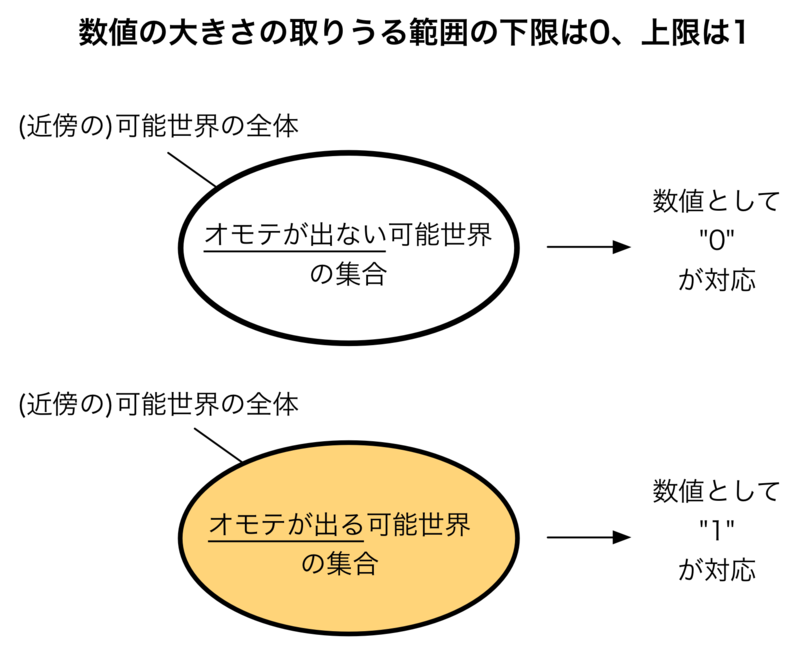
というイメージです。このとき、両者の中間のケースとなる「(近傍の)可能世界の全体における一部の可能世界がオモテが出る可能世界である」という場合には、0から1の間の数値が対応すると考えるのがしっくりくるかと思います。

はい。
さて、では『「オモテが出る可能世界(Aが真である可能世界)の集合」に数値(実数)を対応させる』というアプローチ自体を図で描いてみたいと思います。いささか抽象的になりますが:
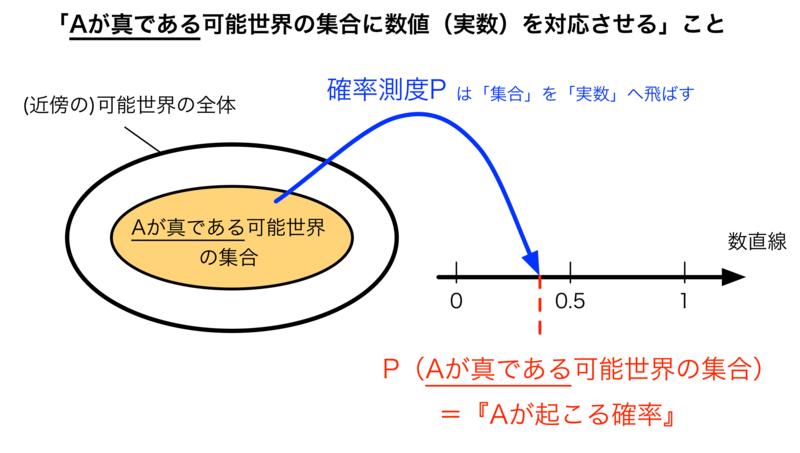
のように描けるかと思います。このとき、この上図における「P」 は「部分集合に対して実数を対応させる関数」であり、「確率測度」と呼ばれるものになります。そして、その関数により与えられた値である「P(Aが真である可能世界の集合)」が「Aの確率」となります。
抽象的すぎて分かりにくいかもしれないので、具体例で考えてみましょう。例えば、「今から私が百円硬貨を投げたときにオモテが出る確率が0.5である」というのは、上記の枠組みにおいて、「P(今から私が百円硬貨を投げたときにオモテが出る可能世界の集合) = 0.5」に対応します。「P」 は「今から私が百円硬貨を投げたときにオモテが出る可能世界の集合に対して、0.5という実数を対応させる関数」となっています。(ここで”0.5”という数字が対応することの正当性については、確率の「規格」ではなく「内実」の方に関わる問題になります*3)
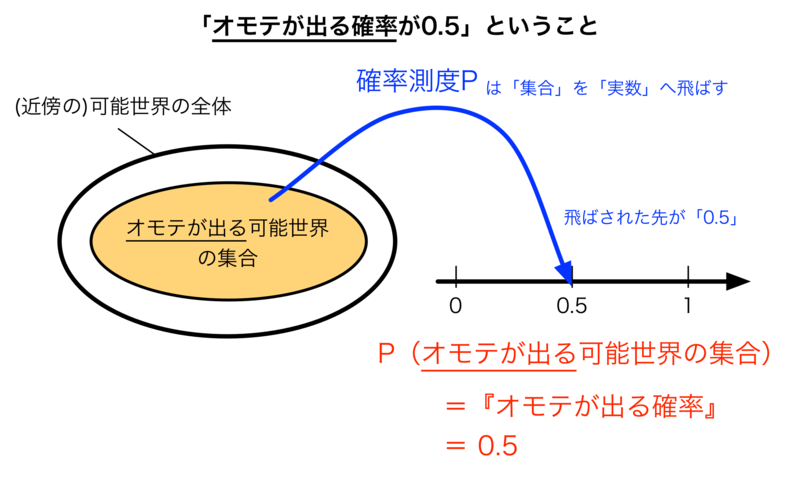
上記のように、ある「部分集合に対して実数を対応させる関数」によって「確率」を定式化するのが測度論的確率論の基本的な考え方になります。
測度論的確率論では通常、上記の「部分集合」が含まれる「全体」に関しては、今回のような「可能世界の集合」という言い方はせずに、「諸事象の全体」としての抽象的な「確率空間」というものを最初に想定した説明がなされます。逆に言うと、その「確率空間」と「様相論理/可能世界論」のパラレリズムを明示的に意識しながら確率測度について説明する、というのが今回の記事の骨子となっています(参考→: at_akadaさんによる「確率空間」と「可能世界論」の読み替えメモの記事)。
ここで「測度」というのは「大きさ」というものに関する一般的な概念であり、例えば、数学的には「面積」というものは、2つ組の実数からなるユークリッド空間全体における「部分集合」に対して実数を対応させる関数(測度)により定式化されています。この「面積」と同様に、「確率」は数学的には「確率空間/可能世界全体」における「部分集合」に対して実数を対応させる関数(確率測度P)によって定式化されているわけです。
で。
もちろん、その「部分集合に対して実数を対応させる関数(確率測度P)」というものは「関数だったらなんでもよい」というわけではありません。「確率測度」と呼ばれるためにには、以下の「コルモゴロフによる確率の公理」の要件を満たしている必要があります。
というわけで、「コルモゴロフによる確率の公理」について以下で見ていきましょう。
(とは言っても、実は、これまでの「確率」の説明においてあらかじめ確率の公理の要件を満たすように話を進めてきているので、実質的にはおさらいの形になります)
コルモゴロフによる確率の公理
Wikipedia先生によるとコルモゴロフによる確率の公理は次の通りです:
確率測度の定義は、コルモゴロフによる次のような確率の公理の形にまとめることが出来る。
- 第一公理: 全ての事象の起きる確率は 0 以上 1 以下である; 0 ≤ P(E) ≤ 1 for all E ∈ E 。
- 第二公理: 全事象 S の起きる確率は 1 である; P(S) = 1 。
- 第三公理: 可算個の排反事象に関する和の法則が成り立つ; {Ek}k∈N が、どの二つも互いに共通部分を持たないような E の元の可算列ならば
この第一公理は、任意の事象E(= 任意の(近傍の)可能世界の部分集合E)に関してその確率P(E)は「0以上1以下」になるというものです*4。具体的に言うと、P(今から私が百円硬貨を投げたときにオモテが出る)が「0以上1以下」の範囲の値である、ということになります。本記事の説明においても、P(近傍の可能世界の部分集合)は「0以上1以下」範囲の値をとるとしているので、この公理が満たされています。
次の第二公理は、「全事象の確率は1である」というものです。本記事の説明においても、P(近傍の可能世界の全体)= 1としているので、この定理が満たされています。
最後の第三公理は、各事象(=近傍の可能世界における各部分集合)に重なりがない(排反な)場合に、確率の「足し算」が成り立つということです。これは例えば、事象A(=Aが真である可能世界の集合)と事象B(=Bが真である可能世界の集合)に重なりがない場合に、P(A ∨ B) = P(A) + P(B)が成り立つというものです。P(A)とP(B)がそれぞれ事象Aと事象Bの確率空間(=可能世界の全体)内における"面積"のようなものに対応するものと考えれば、この足し算が成り立つのは自然なものであると考えられます。
はい。
というわけで、今回の記事では:
「可能である」ということは、「この現実世界@」の近傍の可能世界の集合の枠組みにより表すことができる
というところから出発し、コルモゴロフによる確率の公理までたどり着くことができました。
(もし説明が煩雑すぎて途中で遭難してしまっていたらすみません。。)
今回のまとめ
はい。
では、今回の内容をまとめます:
- 「可能である」ということは「(近傍の)可能世界全体の部分集合」の形で捉えることができる
- 様相論理の理路から「確率空間」を捉えることがもし許容されるならば*5、以下のように「確率」を捉えることができる
- ざっくり言うと:「Aの確率」とは、(近傍の)可能世界全体における「Aが真である可能世界の部分集合」の「大きさ」である
- もうちょい細かく言うと:(近傍の)可能世界全体において、関数Pが以下の3つの要件を満たすとき、P(Aが真である近傍の可能世界の集合)は「Aの確率」である
- 0 ≦ P(近傍の可能世界の部分集合)≦ 1
- P(近傍の可能世界の全体)= 1
- 「Aが真である近傍の可能世界の集合」と「Bが真である近傍の可能世界の集合」に重なりがないとき、P(Aが真である近傍の可能世界の集合 ∨ Bが真である近傍の可能世界の集合)= P(Aが真である近傍の可能世界の集合) + P(Bが真である近傍の可能世界の集合)
はい。こんなかんじでしょうか。
で。
あのですね。
もしかすると、数学のセカイから「確率」を眺めている方々にとっては、今回の記事は「野暮の極み」に映っているのかもと想像しています。
なぜかというと、そもそもこういう可能世界論みたいな「哲学的なんちゃらかんちゃら」との関わりあいをキレイに避けられるのが「確率空間」とか「確率測度」みたいなものを援用して考えることの利点でもあるからです。
まあそれは確かにそうなのです。ですが、実務的な観点から言いますと、可能世界論から「確率」を捉えることには:
「可能である」という概念と「確率」概念のあいだのギャップ
を明晰に理解できるようになるという、大きな利点もあるのです。
この「ギャップ」を理解しておくことは、現実のナマナマしい案件を確率論的モデリングの世界に落とし込む際にとても重要になります。
今回の記事の後編として、次回の記事ではその『「可能である」という概念と「確率」概念のあいだのギャップ』について書いていきたいと思います。
<参考文献>

- 作者: 平岡和幸,堀玄
- 出版社/メーカー: オーム社
- 発売日: 2009/10/20
- メディア: 単行本(ソフトカバー)
- 購入: 10人 クリック: 133回
- この商品を含むブログ (28件) を見る

- 作者: 中塚利直
- 出版社/メーカー: 岩波書店
- 発売日: 2010/06/19
- メディア: 単行本(ソフトカバー)
- 購入: 2人 クリック: 16回
- この商品を含むブログ (3件) を見る
<参考サイト>
雑記2008年3月26日(水) - うつし世はゆめ / 夜のゆめもゆめ
at-akadaさんによる可能世界論と確率空間の読み替えについてのメモです。参考にさせていただきました。多謝です。
.